









The Cross-Product of two vectors is a fundamental concept in vector algebra with significant applications in physics, engineering, and computer science. It provides insights into the perpendicular vector and is essential in understanding rotational forces and torques.
- 1. Introduction to the Cross Product of two vectors
- 2. Definition of the Cross Product of two vectors
- 3. Meaning of the Cross Product of Two Vectors
- 4. Cross Product of two vectors Formula
- 5. Right Hand Rule for the Cross Product
- 6. Properties of the Cross Product of two vectors
- 7. Cross Product of Three vectors
- 8. Examples related to Cross Product of Two Vectors
- 9. Practice Questions related to Cross Product of Two Vectors
- 10. FAQs
- 11. Applications of the Cross Product of Two Vectors
- 12. Conclusion
1. Introduction to the Cross Product of two vectors
The cross product, also known as the vector product, is a crucial operation in vector algebra. Unlike the dot product, which results in a scalar, the cross product yields a vector perpendicular to the plane formed by the two input vectors. This concept is vital in physics for understanding rotational forces and in engineering for analyzing torques.
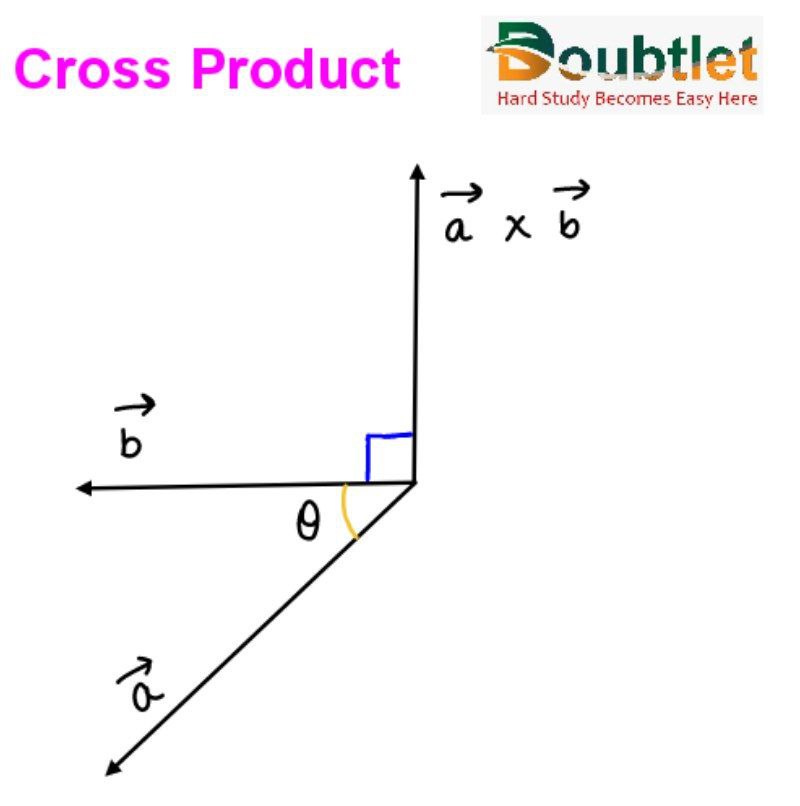
2. Definition of the Cross Product of two vectors
The cross product of two vectors, A and B, denoted as A X B, is a vector perpendicular to A and B.
The magnitude of the cross-product is given by: |A X B| = |A|.|B|.Sin().
Where θ is the acute angle between A and B.
represents the normal vector to the plane containing both vectors.
The right-hand rule determines the direction of the cross-product.
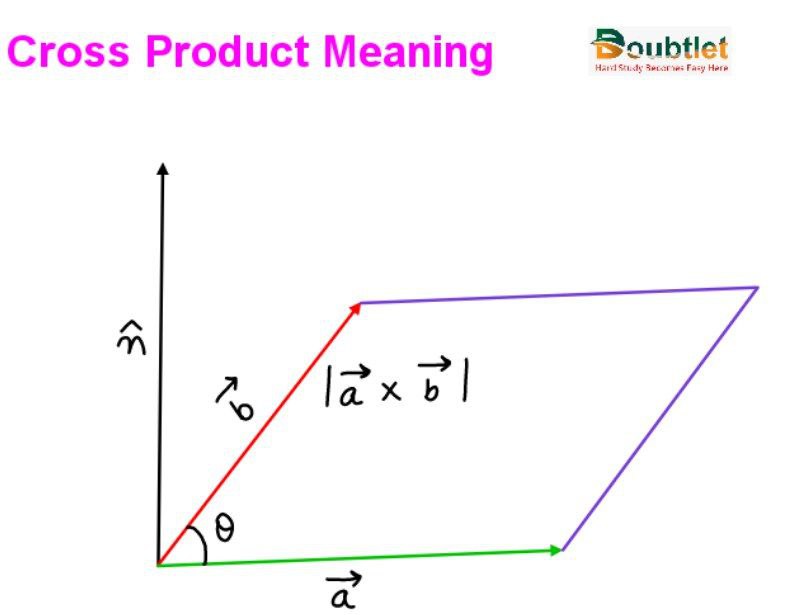
3. Meaning of Cross Product of Two Vectors
The cross product of two vectors, often referred to as the vector product, results in a third vector perpendicular to the plane formed by the original vectors. The magnitude of this resultant vector is proportional to the area of the parallelogram spanned by the two input vectors. This operation is essential in physics and engineering to understand rotational forces and torque.
4. Cross Product of two vectors Formula
To calculate the cross product of two vectors A and B in 3-dimensional space, use the following formula:
A × B =
This results in a new vector C = A × B given by:

C =

Example Calculation
Given two vectors:
The cross product A × B is calculated as follows:
A × B =
A x B = =
5. Right-hand rule for the Cross Product
The right-hand rule is a simple way to determine the direction of the cross-product vector. To use it, point your right hand's index finger toward the first vector (A) and your middle finger toward the second vector (B). Your thumb will then point toward the resultant cross-product vector C = (A × B).

This rule helps visualize the perpendicular direction of the cross-product in three-dimensional space.
6. Properties of the Cross Product of two vectors
Perpendicularity: The resultant vector is perpendicular to both input vectors.
Anticommutativity: A × B = -(B × A)
Distributivity: A × (B C) = A × B A × C
Scalar Multiplication: (kA) × B = k(A × B) = A × (kB)
Cross-Product with Zero Vector: a x 0 = 0
Cross-Product with Itself: a x a = 0
Cross-Product of Unit Vectors:
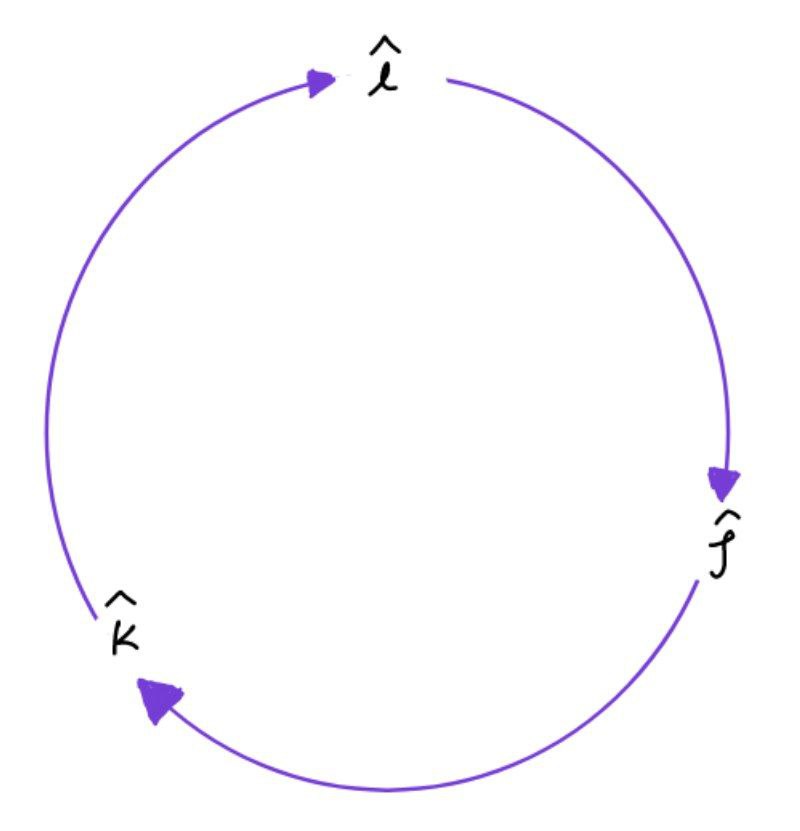
- x = x = x = 0
- x = , x = and x =
- x = -, x = - and x = -
7. Cross Product of Three vectors
(a) Vector Triple Product:
The cross product of a vector with the cross product of the other two vectors is the triple cross product of the vectors. The resultant of the triple cross product is a vector.If a, b and c are the vectors, then the vector triple product is:
(A x B) x C = (A.C)B - (B.C)A
(b) Scalar Triple Product:
The cross product of three vectors, often called the scalar triple product, involves taking the cross product of two vectors and then the dot product of the result with the third vector. Mathematically, vectors A, B, and C are expressed as A·(B×C). This operation yields a scalar value representing the parallelepiped volume formed by the three vectors.
8. Examples related to Cross Product of Two Vectors
Given vectors A = 4i 3j 2k and B = -2i j 3k, find A × B.
A X B =
A X B = =
9. Practice Questions related to Cross Product of Two Vectors
Question 1: Calculate the cross product of A = 2i - j 5k and B = -2i 5j 7k.
Question 2: If A = - i 1.2j - 4k and B = 6i - 5j 9k, find A × B.
10. FAQs
What is the cross-product?
The cross-product of two vectors results in a third vector perpendicular to the plane formed by the original vectors.
How is the cross-product used in physics?
It is used to calculate torque, magnetic forces, and rotational dynamics.
Can the cross-product be zero?
Yes, if the two vectors are parallel or one is a zero vector.
What does the magnitude of the cross-product represent?
It represents the area of the parallelogram formed by the two vectors.
What is the right-hand rule?
A method to determine the direction of the cross-product vector.
Can the cross-product be used in higher dimensions?
The cross product is specifically defined for three-dimensional vectors, but similar operations, like the wedge product, exist for higher dimensions.
How does the cross-product relate to angular momentum?
In physics, the angular momentum of a particle is given by the cross-product of its position vector and its momentum vector.
What is the difference between the dot product and the cross product?
The dot product results in a scalar and measures the magnitude of projection, while the cross product results in a vector perpendicular to the plane of the original vectors.
11. Applications of the Cross Product of Two Vectors
Physics:
(i) Torque Calculation: Torque (τ) is calculated using the cross product of the position vector (r) and the force vector (F):
(ii) Magnetic Force: The force on a charged particle moving in a magnetic field is given by:
Engineering
(i) Moment of a Force: Used to determine the moment of a force about a point.
(ii) Rotational Dynamics: Essential for analyzing rotating systems.
12. Conclusion
Understanding the cross-product of two vectors equips you with essential tools for solving problems in physics and engineering. Mastering this concept allows you to analyze rotational systems, calculate torques, and more. Dive deeper into vector algebra, and you'll find the cross-product to be an indispensable ally in your mathematical toolkit.
If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real-time. Sign up and get registered with us.
Linear Algebra Calculators
Cross Product Calculator
Matrix Inverse Calculator
Blog Information
Blog Author: Neetesh Kumar
Blog Publisher: Doubtlet
Comments(0)
Your comment will be reviewed before it is published.




Leave a comment