Understanding Matrix Null Space, Kernel, and Nullity: A Complete Guide

Matrix null space, kernel, and nullity are fundamental concepts in linear algebra that help describe the behavior of linear transformations. The null space (or kernel) is the set of vectors mapped to the zero vector by a matrix, and the nullity is the dimension of this null space. Together, they provide insight into the structure and rank of matrices, helping to solve systems of linear equations and analyze transformations.

Get Homework Help

1. Introduction to the Matrix Null Space, Kernel, and Nullity:

In linear algebra the concepts of null space, kernel, and nullity are essential when analyzing matrices and their transformations. These ideas help us understand how linear transformations behave, particularly regarding what vectors are "lost" or "sent to zero" during the transformation. Whether you're studying linear equations or computer graphics, grasping these concepts will deepen your understanding of the nature of matrices and their operations.

2. What is Matrix Null Space, Kernel, and Nullity:

• Null Space: The null space of a matrix ${A}$, denoted as ${N(A)}$, is the set of all vectors ${x}$ such that ${Ax=0}$. It contains all the vectors that the matrix maps to the zero vector.

• Kernel: The kernel is used interchangeably with null space in linear transformations. For a linear transformation ${T: V \to W}$, the kernel is the set of all vectors in ${V}$ that are mapped to the zero vector in ${W}$, i.e., Ker${(T)= \{v \in V \mid T (v) = 0 \}}$.

• Nullity: Nullity is the dimension of the null space of a matrix. If the null space contains multiple vectors, the nullity counts how many linearly independent vectors form a basis for the null space. Nullity can be understood as a measure of how much information is "lost" when a matrix transformation is applied.

3. How to Find the Matrix Null Space, Kernel, and Nullity:

To find the null space, kernel, and nullity of a matrix:

Step 1: Write the matrix equation
For a given matrix ${A}$, the goal is to solve the equation ${Ax=0}$, where ${x}$ is the vector we want to find.

Step 2: Row reduce the matrix
Reduce the matrix ${A}$ to its row echelon form (or reduced row echelon form) to simplify the system of equations.

Step 3: Solve for the null space
Solve the system of linear equations that result from the reduced matrix. The solutions form the null space, which consists of all vectors ${x}$ that satisfy ${Ax=0}$.

Step 4: Identify the kernel
For a matrix viewed as a linear transformation, the null space is referred to as the kernel. The process for finding the kernel is the same as finding the null space.

Step 5: Calculate the nullity
The nullity is the number of free variables (parameters) in the solution to the system ${Ax=0}$. To determine this, count the number of columns in the matrix minus the rank of the matrix (the number of pivot columns).

4. Rules for Matrix Null Space, Kernel, and Nullity:

Here are some important rules and points to keep in mind:

• Matrix Size: Null space and nullity are defined for ${m \times n}$ matrices, where the number of columns ${n}$ is greater than or equal to the number of rows ${m}$.

• Zero Matrix: If ${A}$ is a zero matrix, the null space is the entire space ${ \R^n }$ (for an ${n}$-column matrix), and the nullity is ${n}$.

• Full Rank: If a matrix ${A}$ has full rank (the maximum possible rank), its nullity is zero, meaning its null space contains only the zero vector.

• Dimension Theorem: The rank-nullity theorem states that for a matrix ${A}$ with ${n}$ columns, the rank of ${A}$ plus the nullity of ${A}$ is equal to ${n}$. rank$(A)$ nullity$(A)=n$

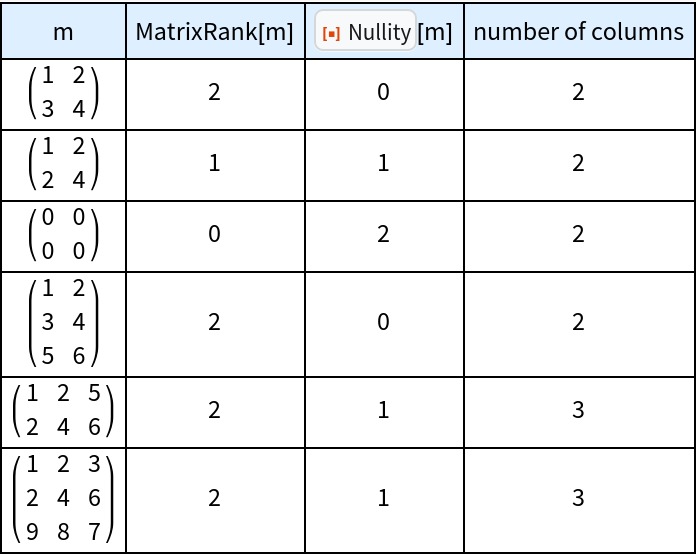
5. Properties of Matrix Null Space, Kernel, and Nullity:

Key properties include:

Null Space:

• The null space is a vector space.
• It contains the zero vector and possibly other vectors.
• Every matrix has a null space, but the null space may consist only of the zero vector.

Kernel:

• The kernel is a subspace of the domain space.
• It can be thought of as the set of all vectors that are annihilated by the matrix (or transformation).

Nullity:

• Nullity is always non-negative.
• Nullity measures the dimension of the null space, giving a count of how many independent directions the matrix "collapses."

Relation to Rank:

• The rank-nullity theorem relates the nullity of a matrix to its rank: rank${(A) }$ nullity${(A)=n}$.
• If the nullity is zero, the matrix is injective (one-to-one) for linear transformations.

6. Matrix Null Space, Kernel, and Nullity Solved Examples:

Question: 1
Null Space and Nullity of a ${2 \times 2}$ Matrix: $A=\begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}$

Solution:

Step 1: Equation ${Ax=0}$

We need to solve: $A \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}$

This gives us the system of equations: $\begin{matrix} 1x_1 2x_2=0 \\ 2x_1 4x_2=0 \end{matrix}$

Step 2: augmented matrix and reduce it: $\begin{bmatrix} 1 & 2 & 0 \\ 2 & 4 & 0 \end{bmatrix} \backsim \begin{bmatrix} 1 & 2 & 0 \\ 0 & 0 & 0 \end{bmatrix}$

Step 3: The first row gives us the equation ${x_1 2x_2=0}$, or ${x_1=-2x_2}$.

Step 4: The general solution is: $\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} -2x_2 \\ x_2 \end{bmatrix} = x_2 \begin{bmatrix} -2 \\ 1 \end{bmatrix}$

Step 5: null space and nullity

• Null space: ${N(A) }$ span $\left\{ \begin{bmatrix} -2 \\ 1 \end{bmatrix} \right\}$
  
• Nullity: ${1}$

Question: 2
Null Space of a ${3 \times 3}$ Matrix: $B=\begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 0 & 0 & 0 \end{bmatrix}$

Solution:

Step 1: Equation ${Bx=0}$

We need to solve: $\begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}$

This gives the system: $\begin{matrix} x_1 2x_2 3x_3=0 \\ x_2 4x_3=0 \end{matrix}$

Step 2: Solve for ${x_2}$ and ${x_1}$
From the second equation: ${x_2= -4x_3}$.
Substitute into the first equation: ${x_1 2(-4x_3) 3x_3 = 0 \implies x_1 - 8x_3 3x_3 = 0 \implies x_1 = 5x_3}$

Step 3: The solution for ${x_1, x_2, x_3}$ is: $\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 5x_3 \\ -4x_3 \\ x_3 \end{bmatrix} = x_3 \begin{bmatrix} 5 \\-4 \\ 1 \end{bmatrix}$

Step 4: null space and nullity

• Null space: ${N(B) }$ span $\left\{ \begin{bmatrix} 5 \\ -4 \\ 1 \end{bmatrix} \right\}$
  
• Nullity: ${1}$

Question: 3
Null Space and Nullity of a ${3 \times 3}$ Matrix: $C=\begin{bmatrix} 1 & 3 & -1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{bmatrix}$

Solution:

Step 1: Equation ${Cx=0}$

We need to solve: $C\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}$

This gives the system: $\begin{matrix} x_1 3x_2-x_3=0 \\ x_2 x_3=0 \end{matrix}$

Step 2: Solve for ${x_2}$ and ${x_1}$
From the second equation: ${x_2= -x_3}$.
Substitute into the first equation: ${x_1 3(-x_3) = 0 \implies x_1 - 3x_3 - x_3 = 0 \implies x_1 = 4x_3}$

Step 3: The solution for ${x_1, x_2, x_3}$ is: $\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 4x_3 \\ -x_3 \\ x_3 \end{bmatrix} = x_3 \begin{bmatrix} 4 \\ -1 \\ 1 \end{bmatrix}$

Step 4: null space and nullity

• Null space: ${N(C) }$ span $\left\{ \begin{bmatrix} 4\\ -1 \\ 1 \end{bmatrix} \right\}$
  
• Nullity: ${1}$

Question: 4
Null Space and Nullity of a ${4 \times 3}$ Matrix: $D=\begin{bmatrix} 1 & 1 & 0 \\ 2 & 2 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix}$

Solution:

Step 1: Equation ${Dx=0}$

We need to solve: $D\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}$

This gives the system: $\begin{matrix} x_1 x_2=0 \\ 2x_1 2x_2=0 \\ x_3=0 \end{matrix}$

Step 2: From the first equation, ${x_1 = - x_2}$.The third equation gives ${x_3=0}$.

Step 3: The general solution is: $\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} -x_2 \\ x_2 \\ 0 \end{bmatrix} = x_2 \begin{bmatrix} -1 \\ 1 \\ 0 \end{bmatrix}$

Step 4: null space and nullity

• Null space: ${N(D) }$ span $\left\{ \begin{bmatrix} -1 \\ 1 \\ 0 \end{bmatrix} \right\}$
  
• Nullity: ${1}$

Question: 5
Kernel and Nullity of a ${2 \times 3}$ Matrix: $E\begin{bmatrix} 2 & 4 & 6 \\ 1 & 2 & 4 \end{bmatrix}$

Solution:

Step 1: Equation ${Ex=0}$

We need to solve: $E \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}$

This gives the system: $\begin{matrix} 2x_1 4x_2 6x_3=0 \\ x_1 2x_2 3x_3=0 \end{matrix}$

Step 2: Perform row reduction on the augmented matrix: $\begin{bmatrix} 2 & 4 & 6 & 0 \\ 1 & 2 & 3 & 0 \end{bmatrix} \backsim \begin{bmatrix} 1 & 2 & 3 & 0 \\ 0 & 0 & 0 &0 \end{bmatrix}$

Step 3: From the row-reduced matrix, we have: ${x_1 2x_2 3x_3=0}$
This gives ${x_1 = -2x_2 - 3x_3}$.

Step 4: The general solution is: $\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} -2x_2 \space \space -3x_3 \\ x_2 \\ x_3 \end{bmatrix} = x_2 \begin{bmatrix} -2 \\ 1 \\ 0 \end{bmatrix} x_3 \begin{bmatrix} -3 \\ 0 \\ 1 \end{bmatrix}$

Step 5: null space and nullity

• Null space: ${N(E) }$ span $\left\{ \begin{bmatrix} -2 \\ 1 \\ 0 \end{bmatrix}, \begin{bmatrix} -3 \\ 0 \\ 1 \end{bmatrix} \right\}$

• Nullity: ${2}$

7. Practice Questions on Matrix Null Space, Kernel, and Nullity:

Q.1 Find the null space and nullity of the matrix: $\begin{bmatrix} 1 & 5 & 2 \\ 3 & 1 & 8 \end{bmatrix}$

Q.2 For the matrix $\begin{bmatrix} 6 & 4 \\ 3 & 4 \end{bmatrix}$, determine the null space and nullity.

Q.3 Find the kernel of the linear transformation represented by the matrix: $\begin{bmatrix} 1 & 0 & -2 \\ 3 & 1 & 1 \end{bmatrix}$

Q.4 Solve for the null space of $\begin{bmatrix} 4 & 7 \\ 6 & 8 \end{bmatrix}$ and find the nullity.

8. FAQs on Matrix Null Space, Kernel, and Nullity:

What is the null space of a matrix?

The null space of a matrix is the set of all vectors that, when multiplied by the matrix, result in the zero vector.

What is the kernel of a matrix?

The kernel is another term for the null space, specifically when referring to linear transformations.

How do you find the nullity of a matrix?

The nullity is the dimension of the null space and is found by subtracting the rank of the matrix from the total number of columns.

What does it mean if the nullity is zero?

A nullity of zero means that the matrix has full rank and its null space contains only the zero vector.

What is the relationship between rank and nullity?

According to the rank-nullity theorem, the sum of the rank and the nullity of a matrix equals the number of columns in the matrix.

Is the null space always non-empty?

Yes, the null space always contains at least the zero vector.

Can the null space contain more than one vector?

Yes, the null space can contain an infinite number of vectors if the matrix has a nullity greater than zero.

9. Real-life application of Matrix Null Space, Kernel, and Nullity:

• Engineering: The null space is used to find the modes of mechanical systems that result in no net movement, crucial for analyzing structures and mechanical vibrations.

• Computer Graphics: In graphics, null spaces can represent the portions of transformations that result in the compression or elimination of certain visual elements.

• Data Science: In machine learning, understanding the null space helps with dimensionality reduction, identifying redundant features, and avoiding overfitting.

• Network Theory: Nullity is used in network flow problems to find redundancies in systems or to optimize routes by identifying elements that do not contribute to the solution.

10. Conclusion:

Matrix null space, kernel, and nullity are powerful concepts in linear algebra that offer insight into the behavior of matrix transformations. They help explain how and why certain vectors are mapped to zero, and they are central to understanding the rank and efficiency of a matrix. Mastering these concepts opens the door to solving complex problems in engineering, computer science, and beyond. By applying these techniques, you can analyze matrices more effectively and solve a wide range of practical problems.

If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]

$\fcolorbox{black}{lightpink}{\color{blue}{Get Assignment Help}}$
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real-time. Sign up and get registered with us.

$\color{red} \bold{Related \space Pages:}$
Matrix Adjoint Calculator
Matrix Formula Sheet
Linear Algebra Calculators
Matrix Inverse Calculator
Matrix Scalar Multiplication Calculator