Partial Fraction Decomposition: Step-by-Step Guide, Examples, and Applications

Partial Fraction Decomposition is a method that breaks down complex rational expressions into simpler fractions, making them easier to integrate or simplify. It is particularly useful in calculus and algebra, where simplifying expressions helps solve integrals, differential, and algebraic equations more efficiently.

Get Homework Help

1. Introduction to the Partial Fraction Decomposition:

Partial Fraction Decomposition is a crucial algebraic technique used to simplify complex rational expressions by breaking them down into simpler fractions. This method is especially helpful in integration, solving differential equations, and simplifying algebraic fractions. It allows you to express a rational function as the sum of simpler fractions, making the overall problem easier to handle.

2. What is Partial Fraction Decomposition:

Partial Fraction Decomposition is the process of expressing a given rational function, typically of the form $\frac{P(x)}{Q(x)}$ where ${P(x)}$ and ${Q(x)}$ are polynomials, as the sum of simpler fractions. These fractions will have a simpler denominator, making further calculations more straightforward.

For example: $\dfrac{3x+5}{(x-1)(x+2)} = \dfrac{A}{x-1} + \dfrac{B}{x+2}$

Where ${A}$ and ${B}$ are constants to be determined.

3. How to Find the Partial Fraction Decomposition:

To find the Partial Fraction Decomposition of a rational function, follow these steps:

Step 1: Factor the Denominator

• Factor the denominator of the rational expression into its irreducible factors.

Step 2: Set Up the Decomposition

• For each distinct linear factor ${(x-c)}$, include a term like ${\dfrac{A}{x-c}}$.

• For each repeated factor ${(x-c)^n}$, include terms like ${\dfrac{A_1}{x-c} + \dfrac{A_2}{(x-c)^2} + \cdots + \dfrac{A_n}{(x-c)^n}}$.

• For irreducible quadratic factors ${ax^2 + bx + c}$ use terms like ${\dfrac{Ax + B}{ax^2 + bx + c}}$.

Step 3: Multiply Through by the Denominator

• Multiply both sides of the equation by the original denominator to eliminate the fractions.

Step 4: Solve for the Unknowns

• Expand and simplify the resulting equation, then solve for the constants ${A, B, C, \cdots}$.

Step 5: Substitute the Constants

• Substitute the values of the constants back into the partial fraction form to complete the decomposition.

4. Table for Partial Fraction Decomposition:

S.No.	Rational function	Form of the partial fraction
1	$\dfrac{px + q}{(x-a)(x-b)}$, where $a \neq b \ \ \ \ \ \ \ \$	$\dfrac{A}{x-a} + \dfrac{B}{x-b}$
2	$\dfrac{px + q}{(x-a)^2}$	$\dfrac{A}{x-a} + \dfrac{B}{(x-a)^2}$
3	$\dfrac{px^2 + qx + r}{(x-a)(x-b)(x-c)}$	$\dfrac{A}{x-a} + \dfrac{B}{x-b} + \dfrac{C}{x-c}$
4	$\dfrac{px^2 + qx + r}{(x-a)^2(x-b)}$	$\dfrac{A}{x-a} + \dfrac{B}{(x-a)^2} + \dfrac{C}{x-b}$
5	$\dfrac{px^2 + qx + r}{(x-a)(x^2 + bx + c)}$	$\dfrac{A}{x-a} + \dfrac{Bx + C}{x^2 + bx +c}$

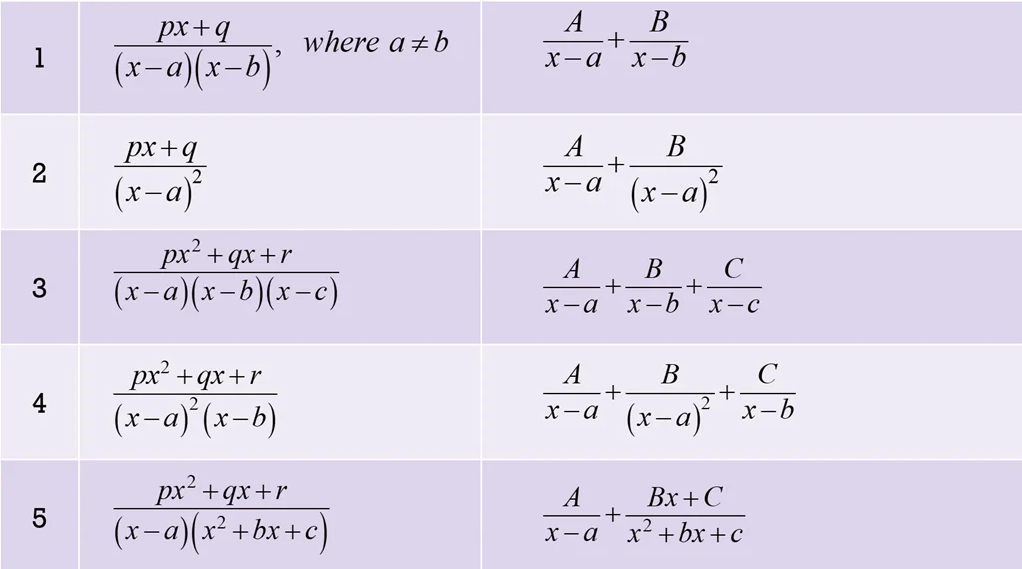
General Rules to Follow

• Here are the essential rules to follow when performing Partial Fraction Decomposition:

• Proper Rational Functions: Partial fraction decomposition only applies to proper rational functions, where the degree of the numerator is less than the degree of the denominator. If the function is improper, perform polynomial division first.

• Distinct Linear Factors: For distinct linear factors like ${(x-a)}$, the decomposition uses simple fractions ${\dfrac{A}{x-a}}$.

• Repeated Linear Factors: For repeated linear factors like ${(x-a)^n}$, include fractions like ${\dfrac{A_1}{x-a} + \dfrac{A_2}{(x-a)^2} + \cdots + \dfrac{A_n}{(x-a)^n}}$.

• Irreducible Quadratic Factors: For irreducible quadratic factors like ${ax^2 + bx + c}$, the corresponding terms should have numerators of the form ${Ax + B}$.

• Non-factorable Quadratics: If the denominator includes non-factorable quadratic expressions, include terms like $\dfrac{Ax + B}{ax^2 + bx + c}$.

5. Properties of Partial Fraction Decomposition:

The process of Partial Fraction Decomposition has several important properties:

• Uniqueness: For any proper rational function, the partial fraction decomposition is unique (except for ordering terms).

• Additive Property: If you decompose two rational functions and then add them, their sum can be decomposed by adding the decomposed forms.

• Integral Compatibility: Partial fraction decomposition is a highly useful tool for simplifying integrals, particularly for rational functions that are hard to integrate directly.

• Reduces Complexity: This method breaks down complex rational expressions into simpler components, making algebraic manipulation and integration more manageable.

6. Partial Fraction Decomposition Solved Examples:

Question: 1
Decompose: ${\dfrac{3x + 5}{(x-1)(x + 2)}}$ using partial fraction method.

Solution:

Step 1: The denominator is already factored as ${(x-1)(x + 2)}$.

Step 2: ${\dfrac{3x + 5}{(x-1)(x + 2)} = \dfrac{A}{x-1} \dfrac{B}{x 2}}$

Step 3: Multiply both sides by ${(x-1)(x + 2)}$ to clear the fractions:
${3x + 5 = A(x + 2) + B(x-1)}$

Step 4: Expand both sides: ${3x + 5 = A(x) + 2A + B(x) - B = (A + B)x + (2A-B)}$

Step 5: Compare coefficients of ${x}$ and the constant terms:

• Coefficients of ${x:A + B=3}$
  
• Constant terms: ${2A-B=5}$

Solve the system:

1. ${A + B=3}$
   
2. ${2A-B=5}$

We can solve the above system of linear equations by this Calculator

From ${A + B=3}$, we get ${B=3-A}$.

Substitute into ${2A-B=5}$:
${2A - (3-A) = 5 \implies 3A=8 \implies A = \dfrac{8}{3}}$

Substitute ${A = \frac{8}{3}}$ into ${B=3-A}$:
${B=3 - \dfrac{8}{3} = \dfrac{9}{3} - \dfrac{8}{3} = \dfrac{1}{3}}$

Step 6: ${\dfrac{3x 5}{(x-1)(x+2)} = \dfrac{\frac{8}{3}}{x - 1} + \dfrac{\frac{1}{3}}{x + 2}}$

Question: 2
Decompose $\dfrac{2x + 3}{(x + 1)^2}$ using partial fraction method.

Solution:

Step 1: The denominator is ${(x + 1)^2}$, a repeated linear factor.

Step 2: ${\dfrac{2x + 3}{(x + 1)^2} = \dfrac{A}{x + 1} \dfrac{B}{(x + 1)^2}}$

Step 3: Multiply both sides by ${(x + 1)^2}$: ${2x + 3 = A(x + 1) B}$

Step 4: Expand the right-hand side: ${2x + 3 = A(x) + A + B = Ax + (A + B)}$

Step 5: Compare coefficients of ${x}$ and the constant terms:

• Coefficient of ${x}$: ${A=2}$
  
• Constant term: ${A + B=3}$

Substitute ${A=2}$ into ${A + B=3}$: ${2 + B=3 \implies B=1}$

Step 6: ${\dfrac{2x + 3}{(x + 1)^2} = \dfrac{2}{x + 1} + \dfrac{1}{(x + 1)^2}}$

Question:3
Decompose ${\dfrac{x^2+x+1}{(x+1)(x-2)}}$ using partial fraction method.

Solution:

Step 1: The denominator is already factored as ${(x+1)(x-2)}$.

Step 2: ${\dfrac{x^2+x+1}{(x+1)(x-2)} = 1 \dfrac{2x+3}{(x+1)(x-2)}}$

${\dfrac{2x+3}{(x+1)(x-2)} = \dfrac{A}{x+1} + \dfrac{B}{x-2}}$

Step 3: Multiply both sides by ${(x+1)(x-2)}$:
${x^2+x+1 = A(x-2)+B(x+1)}$

Step 4: Expand the right-hand side: ${x^2+x+1 = A(x)-2A+B(x)+B = (A+B)x+(-2A+B)}$

Step 5: Compare coefficients of ${x}$ and the constant terms:

• Coefficient of ${x}$: ${A+B=1}$
• Constant term: ${-2A+B=1}$

Solve the system:

1. ${A+B=1}$
2. ${-2A+B=1}$

We can solve the above system of linear equations by this Calculator

After solving we get $A = -\frac{1}{3}, B = \frac{7}{3}$

Step 6: ${\dfrac{x^2+x+1}{(x+1)(x-2)} = 1 + \dfrac{-\frac{1}{3}}{x+1} + \dfrac{\frac{7}{3}}{x-2}}$

Question:4
Decompose ${\dfrac{6x^2+7x+3}{(x+1)(x-1)^2}}$ using partial fraction method.

Solution:

Step 1: The denominator is $(x+ 1)(x-1)^2$, which includes a repeated linear factor.

Step 2: ${\dfrac{6x^2+7x+3}{(x+1)(x-1)^2} = \dfrac{A}{x+1} + \dfrac{B}{x-1} + \dfrac{C}{(x-1)^2}}$

Step 3: Multiply both sides by ${(x+1)(x-1)^2}$:
${6x^2+7x+3=A(x-1)^2 B(x+1)(x-1) C(x+1)}$

Step 4: Expand each term on the right-hand side:
${A(x-1)^2 = A(x^2-2x+1)}$
${B(x+1)(x-1)=B(x^2-1)}$
${C(x+1)=Cx+C}$
Combine everything:
${6x^2+7x+3=A(x^2-2x+1) B(x^2-1)+Cx+C}$
${6x^2+7x+3=(A+B)x^2+(-2A+C)x+(A-B+C)}$

Step 5: Compare coefficients:

• Coefficient of ${x^2}$: ${A+B=6}$
• Coefficient of ${x}$: ${-2A+C=7}$
• Constant term: ${A-B+C=3}$

Solve the system:

1. ${A+B=6}$
2. ${-2A+C=7}$
3. ${A-B+C=3}$

From ${A+B=6, B=6-A}$.

Substitute into ${A-B+C=3}$:
${A-(6-A)+C=3 \implies 2A+C=9}$

Now solve ${-2A+C=7}$ and ${2A+C=9}$. Subtracting the first equation from the second:
${(2A+C)-(-2A+C)=9-7 \implies 4A=2 \implies A= \dfrac{1}{2}}$

Substitute ${A = \frac{1}{2}}$ into ${B=6-A}$:
${B=6- \dfrac{1}{2} = \dfrac{11}{2}}$

Substitute ${A = \frac{1}{2}}$ into ${-2A+C=7}$:
${-2 \bigg(\dfrac{1}{2}\bigg) + C = \implies -1+C=7 \implies C=8 }$

Step 6: ${\dfrac{6x^2+7x+3}{(x+1)(x-1)^2}} = {\dfrac{\frac{1}{2}}{x+1} \dfrac{\frac{11}{2}}{x-1} + \dfrac{8}{(x-1)^2}}$

Question:5
Decompose ${\dfrac{3x^3+4x^2+5x+2}{(x-2)(x^2+1)}}$ using partial fraction method.

Solution:
Step 1: The denominator is ${(x-2)(x^2+1)}$, with a linear factor ${(x-2)}$ and an irreducible quadratic factor ${(x^2+1)}$.

${\dfrac{3x^3+4x^2+5x+2}{(x-2)(x^2+1)} = 3 + \dfrac{10x^2+2x+8}{(x-2)(x^2+1)}}$

Step 2: ${\dfrac{10x^2+2x+8}{(x-2)(x^2+1)} = \dfrac{A}{x-2} + \dfrac{Bx+C}{x^2+1}}$

Step 3: Multiply both sides by ${(x-2)(x^2+1)}$:
${3x^3+4x^2+5x+2=A(x^2+1) (Bx+C)(x-2)}$

Step 4: Expand both sides:
${A(x^2+1)=Ax^2+A}$
${(Bx+C)(x-2) = Bx^2-2Bx + Cx-2C}$

Combine everything:
${10x^2+2x+8=(A+B)x^2+(-2B+C)x+(A-2C)}$

Step 5: Compare coefficients:

• Coefficient of ${x^3}$: No ${x^3}$ term on the right, so no equation for this.
• Coefficient of ${x^2}$: ${A+B=10}$
• Coefficient of ${x}$: ${-2B+C=2}$
• Constant term: ${A-2C=8}$

Solve the system:

1. ${A+B=10}$
2. ${-2B+C=2}$
3. ${A-2C=8}$

We can solve the above system of linear equations by this Calculator

So, we get $A = \dfrac{52}{5}, B = -\dfrac{2}{5}, C = \dfrac{6}{5}$

Step 6: ${\dfrac{10x^2+2x+8}{(x-2)(x^2+1)} = 3+ \dfrac{\frac{52}{5}}{x-2} + \dfrac{\frac{6}{5} -\frac{2x}{5}}{x^2+1}}$

so, the partial fraction decomposition is

${\dfrac{3x^3+4x^2+5x+2}{(x-2)(x^2+1)} = 3 + \dfrac{\frac{52}{5}}{x-2} + \dfrac{\frac{2x}{5} - \frac{6}{5}}{x^2+1}}$

7. Practice Questions on Partial Fraction Decomposition:

Q.1 Decompose ${\dfrac{7x+9}{(x-3)(x+2)}}$ using partial fraction method.

Q.2 Find the partial fraction decomposition of ${\dfrac{x^2+6x+9}{(x+1)^2(x-4)}}$.

Q.3 Solve for the partial fraction decomposition of ${\dfrac{2x^2+5x+3}{(x^2+4)(x-2)}}$

Q.4 Decompose ${\dfrac{10}{x(x^2+1)}}$ using partial fraction method.

8. FAQs on Partial Fraction Decomposition:

What is Partial Fraction Decomposition used for?

Partial Fraction Decomposition is used to simplify complex rational expressions, making them easier to integrate or solve algebraically.

When do you need to use Partial Fraction Decomposition?

This technique is useful when working with rational functions in calculus (especially integration) and algebra, where you must simplify fractions with polynomial denominators.

Can you decompose improper fractions?

Improper fractions (where the degree of the numerator is greater than or equal to the denominator) must first be simplified using polynomial division before applying Partial Fraction Decomposition.

What happens if the denominator has irreducible quadratics?

If the denominator contains irreducible quadratics, the partial fraction will include terms of the form ${\dfrac{Ax+B}{ax^2+bx+c}}$, where ${A}$ and ${B}$ are constants to be determined.

What if the denominator includes repeated factors?

For repeated linear factors like ${(x-a)^n}$, you must include separate terms for each power of the factor, such as ${\dfrac{A}{x-a} + \dfrac{B}{(x-a)^2} + \cdots}$.

Can you decompose a non-factorable polynomial?

Non-factorable polynomials in the denominator can still be handled by using terms with linear numerators like ${\dfrac{Ax+B}{ax^2+bx+c}}$.

Why is Partial Fraction Decomposition important in calculus?

Partial Fraction Decomposition simplifies the integration of rational functions, transforming them into sums of simpler fractions that are easier to integrate.

9. Real-Life Application of Partial Fraction Decomposition:

Partial Fraction Decomposition has many applications in real life:

• Signal Processing: In electronics and communication systems, partial fraction decomposition breaks down transfer functions into simpler components for easier analysis of system behavior.

• Control Systems: Engineers use this technique to simplify the analysis of systems governed by differential equations.

• Finance and Economics: In quantitative analysis, partial fractions can help solve complex algebraic models used in financial forecasting and optimization problems.

10. Conclusion:

Partial Fraction Decomposition is an essential tool in both algebra and calculus, simplifying the manipulation of rational expressions. By breaking down a complex fraction into simpler terms, this technique facilitates easier integration, differentiation, and problem-solving across various fields of study. Mastering this method opens up a range of mathematical solutions, from solving integrals to analyzing control systems in engineering.

If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]

$\fcolorbox{black}{lightpink}{\color{blue}{Get Assignment Help}}$
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real time. Sign up and get registered with us.

$\color{red} \bold{Related \space Pages:}$
Matrix Adjoint Calculator
Matrix Formula Sheet
Linear Algebra Calculators
Matrix Inverse Calculator
Matrix Scalar Multiplication Calculator