Adjoint of a Matrix Calculator

Get Homework Help

Neetesh Kumar | January 28, 2025 (Updated) $\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space$ Share this Page on:

Matrices play a critical role in mathematics, engineering, and data science. The Adjoint of a Matrix is a powerful concept often used in finding inverses, solving linear equations, and performing advanced computations. Our Adjoint of a Matrix Calculator is designed to simplify these tasks, providing accurate results quickly and effortlessly. Whether you’re a student, researcher, or professional, this tool ensures precision and efficiency.

1. Introduction to the Adjoint of a Matrix

Imagine you're solving a puzzle, and one piece holds the key to the whole picture. That's similar to finding the adjoint of a matrix in mathematics. It's a simple but important concept, especially in linear algebra, with real-world applications in physics, engineering, and more. In this guide, we’ll explore the adjoint matrix, how to find it, and why it matters when using tools like our adjoint matrix calculator.

$\bold{Definition}$
The adjoint of a matrix also called the adjugate matrix, is the transpose of the cofactor matrix of the original matrix. This operation is useful in finding the inverse of matrices, solving systems of linear equations, and other advanced mathematical operations. Our adjoint of a matrix calculator makes it easy to compute the adjoint of any matrix quickly and accurately.

2. What is the Formula used & conditions required?

The main condition for calculating the adjoint of a matrix is that the matrix must be square. This means the matrix must have the same number of rows and columns, such as a 2x2 matrix, 3x3 matrix, or 4x4 matrix. Non-square matrices do not have an adjoint, so our adjoint matrix calculator is designed to handle square matrices only.

Formula for Adjoint:

For a square matrix $A$ of size $n \times n$:

$\text{adj}(A) = \text{Transpose of Cofactor Matrix of } A$

Where:

• Cofactor: For an element $a_{ij}$, the cofactor is:

  $C_{ij} = (-1)^{i+j} \cdot \det(M_{ij})$

  $M_{ij}$ is the minor matrix obtained by removing the $i$-th row and $j$-th column from $A$.

Conditions for Adjoint Calculation:

• The matrix must be square ($n \times n$).
• Determinants of minors must be computable.

For larger matrices, manual calculations can be tedious and prone to error, making a calculator essential.

Adjoint of a Matrix Formula

The adjoint $\text{adj}(B)$ of a square matrix $B$ of order $n \times n$, can be defined as the transpose of the cofactor matrix.

Consider the $2 \times 2$ matrix $B$ with the elements $b_{11}, b_{12}, b_{21}, b_{22}$, and their cofactor elements are $B_{11}, B_{12}, B_{21}, B_{22}$ respectively.

Then, the adjoint of the matrix formula is as follows:

Adjoint Of a Matrix $2 \times 2$

Let $A$ be the $2 \times 2$ matrix and is given by:

$A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$

Then, the adjoint of this matrix is:

$\text{adj} \, A = \begin{bmatrix} A_{11} & A_{21} \\ A_{12} & A_{22} \end{bmatrix}$

Here,

$A_{11} = \text{Cofactor of } a_{11}$

$A_{12} = \text{Cofactor of } a_{12}$

$A_{21} = \text{Cofactor of } a_{21}$

$A_{22} = \text{Cofactor of } a_{22}$

Alternatively, the adj A can also be calculated by interchanging $a_{11}$ and $a_{22}$ and by changing signs of $a_{12}$ and $a_{21}$. This can be shown as:

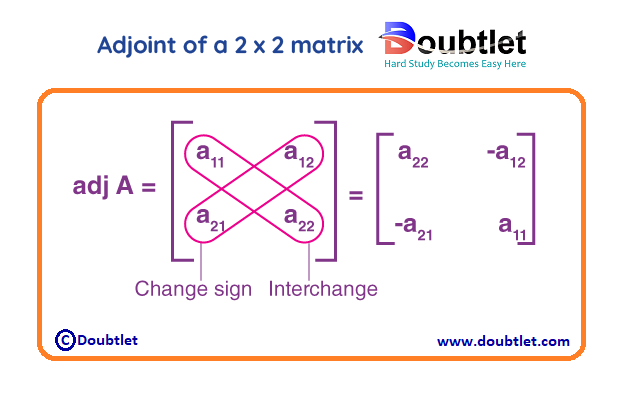
3. How do I calculate the Adjoint of a given matrix?

$\bold{Step \space 1:}$ Begin with a square matrix, denoted as matrix A.
$\bold{Step \space 2:}$ For each element in matrix A, create a new matrix by excluding the row and column that contain the element.
$\bold{Step \space 3:}$ Calculate the $\bold{determinant}$ of each smaller matrix. These determinants are known as cofactors.
$\bold{Step \space 4:}$ Form a new matrix, called the cofactor matrix, using the $\bold{cofactors}$ of each element of matrix A.
$\bold{Step \space 5:}$ Transpose of the cofactor matrix by switching its rows and columns. The resulting matrix is the adjoint of the matrix A.

Using our matrix adjoint calculator, you can automate these steps and receive the solution within seconds, whether a 2x2 matrix, 3x3 matrix, or even a more complex 4x4 matrix.

To manually calculate the adjoint:

1. Find Minors: For each element $a_{ij}$, calculate the determinant of the minor matrix $M_{ij}$.
2. Determine Cofactors: Multiply each minor by $(-1)^{i+j}$.
3. Form the Cofactor Matrix: Arrange the cofactors into a matrix.
4. Transpose the Cofactor Matrix: Swap rows and columns to obtain the adjoint.

Example: Find the Adjoint of a $3 \times 3$ Matrix

Find the adjoint of the matrix:

$A = \begin{bmatrix} 2 & 3 & 1 \\ 4 & 5 & 2 \\ 7 & 8 & 6 \end{bmatrix}$

Solution:

1. Compute the Cofactor Matrix:

For each element $a_{ij}$, calculate the cofactor $C_{ij}$ using minors:

$\text{Cofactor Matrix} = \begin{bmatrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{bmatrix}$

$C_{11} = (-1)^{1+1} \det \begin{bmatrix} 5 & 2 \\ 8 & 6 \end{bmatrix} = 5 \cdot 6 - 2 \cdot 8 = 30 - 16 = 14$

$C_{12} = (-1)^{1+2} \det \begin{bmatrix} 4 & 2 \\ 7 & 6 \end{bmatrix} = - (4 \cdot 6 - 2 \cdot 7) = - (24 - 14) = -10$

$C_{13} = (-1)^{1+3} \det \begin{bmatrix} 4 & 5 \\ 7 & 8 \end{bmatrix} = 4 \cdot 8 - 5 \cdot 7 = 32 - 35 = -3$

$C_{21} = (-1)^{2+1} \det \begin{bmatrix} 3 & 1 \\ 8 & 6 \end{bmatrix} = - (3 \cdot 6 - 1 \cdot 8) = - (18 - 8) = -10$

$C_{22} = (-1)^{2+2} \det \begin{bmatrix} 2 & 1 \\ 7 & 6 \end{bmatrix} = 2 \cdot 6 - 1 \cdot 7 = 12 - 7 = 5$

$C_{23} = (-1)^{2+3} \det \begin{bmatrix} 2 & 3 \\ 7 & 8 \end{bmatrix} = - (2 \cdot 8 - 3 \cdot 7) = - (16 - 21) = 5$

$C_{31} = (-1)^{3+1} \det \begin{bmatrix} 3 & 1 \\ 5 & 6 \end{bmatrix} = 3 \cdot 6 - 1 \cdot 5 = 18 - 5 = 1$

$C_{32} = (-1)^{3+2} \det \begin{bmatrix} 2 & 1 \\ 4 & 6 \end{bmatrix} = - (2 \cdot 6 - 1 \cdot 4) = - (12 - 4) = 0$

$C_{33} = (-1)^{3+3} \det \begin{bmatrix} 2 & 3 \\ 4 & 5 \end{bmatrix} = 2 \cdot 5 - 3 \cdot 4 = 10 - 12 = -2$

Thus, the cofactor matrix is:

Cofactor Matrix: $\begin{bmatrix} 14 & -10 & -3 \\ -10 & 5 & 5 \\ 1 & 0 & -2 \end{bmatrix}$

2. Take the Transpose:

$\text{Adjoint of } A = \left[ \begin{array}{ccc} 14 & -10 & -3 \\ -10 & 5 & 5 \\ 1 & 0 & -2 \end{array} \right]^T$ $= \left[ \begin{array}{ccc} 14 & -10 & 1 \\ -10 & 5 & 0 \\ -3 & 5 & -2 \end{array} \right]$

Final Answer:

$\text{Adjoint of } A = \left[ \begin{array}{ccc} 14 & -10 & 1 \\ -10 & 5 & 0 \\ -3 & 5 & -2 \end{array} \right]$

Our calculator automates this process, ensuring accuracy and efficiency.

4. Why choose our Adjoint of a Matrix Calculator?

$\bold{Easy \space \space to \space Use}$
Our adjoint matrix calculator offers a user-friendly experience. Input your square matrix, and the calculator will compute the adjoint matrix in seconds. This tool simplifies the process, whether you need to find the adjoint of a 2x2 matrix or a 3x3 matrix.

$\bold{Time \space Saving \space By \space automation}$
Calculating the adjoint of a matrix manually can be time-consuming, especially for larger matrices. Our matrix adjugate calculator automates this process, allowing you to focus on more complex problems.

$\bold{Accuracy \space and \space Precision}$
The adjoint matrix formula is calculated based on established mathematical principles, ensuring accurate and error-free results. No need to worry about manual mistakes with our matrix adjoint calculator.

$\bold{Versatility}$
Our calculator supports various matrix sizes, including 2x2 matrices, 3x3 matrices, and 4x4 matrices. Whether you're solving for cofactor matrices or finding the adjugate of a matrix, this tool can handle all your matrix needs.

$\bold{Complementary \space Resources}$
In addition to our adjoint of a matrix calculator, we offer other useful tools like matrix cofactor calculators, inverse matrix calculators, and more. These resources help you master linear algebra, physics, and engineering topics.

5. A detailed video based on the concept of Adjoint of a Matrix.

This video explains how to find the adjoint of a matrix step-by-step, whether you are dealing with a 2x2 matrix, 3x3 matrix, or higher-order matrix.

6. How to use this calculator

To use our adjoint of a matrix calculator, simply:

• Input the elements of your matrix into the calculator.
• Click on the Calculate button.
• The adjoint matrix will be displayed, complete with step-by-step explanations. You can easily access, download, and share the solution.

7. Solved Examples

$\bold{Question:1}$
Let's calculate the Adjoint of the given matrix A = $\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$.
$\bold{Solution}$
The Adjoint matrix of the above-given matrix can be calculated by taking the transpose of the matrix of cofactors, i.e. C = $\begin{bmatrix} 4 & -3 \\ -2 & 1 \end{bmatrix}$
now Adj(A) = $[C]^T$ = $\begin{bmatrix} 4 & -2 \\ -3 & 1 \end{bmatrix}$

$\bold{Question:2}$
Let's calculate the Adjoint of the given matrix $\begin{bmatrix} 1 & 2 & 3 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{bmatrix}$.
$\bold{Solution}$
The Adjoint matrix of the above-given matrix can be calculated by taking the transpose of the matrix of cofactors, i.e. C = $\begin{bmatrix} -3 & 6 & -3 \\ 5 & -10 & \space \space 5 \\ -2 & 4 & -2 \end{bmatrix}$
now Adj(A) = $[C]^T$ = $\begin{bmatrix} -3 & 5 & -2 \\ 6 & -10 & \space \space 4 \\ -3 & 5 & -2 \end{bmatrix}$ 8) = 13.

8. Frequently Asked Questions (FAQs)

What's a square matrix?

A square matrix has an equal number of rows and columns, like 2x2, 3x3, or 4x4 matrices.

Can I find the adjoint of any matrix?

No, the matrix must be square to have an adjoint. Only square matrices have adjoints.

Why is the adjoint useful?

It helps solve tricky equations and is super important in physics and engineering.

What are the cofactors of a matrix?

Cofactors are determinants of smaller matrices formed by removing the row and column of an element. They are used to calculate the adjugate matrix.

Can the adjoint be negative?

Sure, the numbers in the adjoint can be positive, negative, or even zero.

9. What are the Real-life applications?

Matrix transposition has numerous real-life applications, including:
$\bold{Data \space Transformation:}$ In data science, it is essential for reshaping data, making it suitable for various analyses and algorithms.
$\bold{Image \space Processing:}$ It is used to manipulate and transform images, particularly in computer graphics and image editing software.
$\bold{Linear \space Algebra:}$ It is a crucial operation in solving systems of linear equations and finding solutions to problems in physics and engineering.
$\bold{Quantum \space Mechanics:}$ In quantum mechanics, the complex conjugate Adjoint of a matrix plays a crucial role in representing quantum states and operators.

10. Conclusion

Finding the adjoint of a matrix may seem challenging, but with tools like our adjoint matrix calculator, it's much simpler. From solving 2x2 matrices to complex 4x4 matrices, understanding this concept is crucial for tackling problems in physics, engineering, and advanced mathematics. Use our calculator to save time, improve accuracy, and master matrix operations effortlessly.

If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]

$\fcolorbox{black}{lightpink}{\color{blue}{Click here to Ask any Doubt}}$
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real-time. Sign up and get registered with us.

$\color{red} \bold{Related \space Calculators}$
$\bold{Inverse \space of \space a \space matrix}$
$\bold{Transpose \space of \space a \space Matrix}$
$\bold{Rank \space of \space a \space Matrix}$
$\bold{Cramer's \space Rule}$
$\bold{Row \space echelon \space form \space of \space a \space matrix}$
$\bold{Reduced \space Row \space Echelon \space form \space of \space a \space matrix}$