Matrix Basis Calculator

Get Homework Help

Neetesh Kumar | January 31, 2025 (Updated) $\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space$ Share this Page on:

When working with linear algebra, one of the most crucial concepts is the basis of a vector space. It helps define the fundamental structure of vector spaces, making it easier to analyze and understand transformations, dependencies, and linear mappings. Our Matrix Basis Calculator simplifies this process by quickly computing a basis for a set of vectors, saving time and effort for students, researchers, and professionals alike.

1. Introduction to the Basis of a space spanned by the vectors

Have you ever wondered about the fundamental building blocks that define a matrix's behavior? Enter the concept of the basis. In this blog, we'll embark on a journey to demystify the basis of a matrix, exploring its definition, practical applications, and how it lays the groundwork for understanding linear transformations.
$\bold{Definition}$
The basis of a matrix refers to a set of vectors that spans the entire space represented by the matrix. These vectors are linearly independent, meaning they can't be expressed as a combination of others in the set. In essence, the basis forms the foundation upon which the matrix operates.

2. What is the Formulae used & conditions required?

$\bold{Formula \space used}$
The basis of a matrix is determined by finding a set of linearly independent vectors that span the matrix's column space. $\bold{Conditions \space required}$
The conditions for a basis include ensuring the vectors are linearly independent and cover the entire column space of the matrix.

Finding the Basis of a Vector Space

To compute the basis of a vector space, we use Gaussian elimination and row-reduction techniques. The basis of the column space of a matrix is found using:

$\text{Basis} = \{\text{Linearly independent column vectors of the matrix}\}$

Steps to Compute the Basis:

1. Forming a Matrix: Arrange the given vectors as rows or columns.
2. Row Reduction (Row Echelon Form or Reduced Row Echelon Form - RREF): Use Gaussian elimination to eliminate dependent rows.
3. Identifying the Basis:
   • The remaining non-zero row vectors (if row-reduced) or
   • Pivot columns (if column-based) form the basis.

Conditions Required:

• The matrix must be non-empty and consist of numerical entries.
• The rank of the matrix determines the number of basis vectors.
• The basis vectors must be linearly independent and must span the vector space.

3. How do I calculate the Basis of a space spanned by the vectors?

The basis of a matrix can be obtained by finding the row space or column space of the matrix formed by a given vector space.

Manually Computing the Basis of a Vector Space

To manually compute the basis of a vector space, follow these steps:

Step 1: Arrange Vectors in a Matrix

Example: Given vectors $v_1, v_2, v_3$, arrange them as rows of a matrix:

$A = \begin{bmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{bmatrix}$

Step 2: Perform Row Reduction (Gaussian Elimination)

Convert the matrix into row echelon form (REF) or reduced row echelon form (RREF):

$\begin{bmatrix} 1 & 2 & 3 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}$

Step 3: Identify Linearly Independent Rows or Columns

Since only one non-zero row remains, the basis consists of one vector:

$\text{Basis} = \{(1,2,3)\}$

For large matrices or complex datasets, our Matrix Basis Calculator automates this entire process, ensuring accuracy and efficiency.

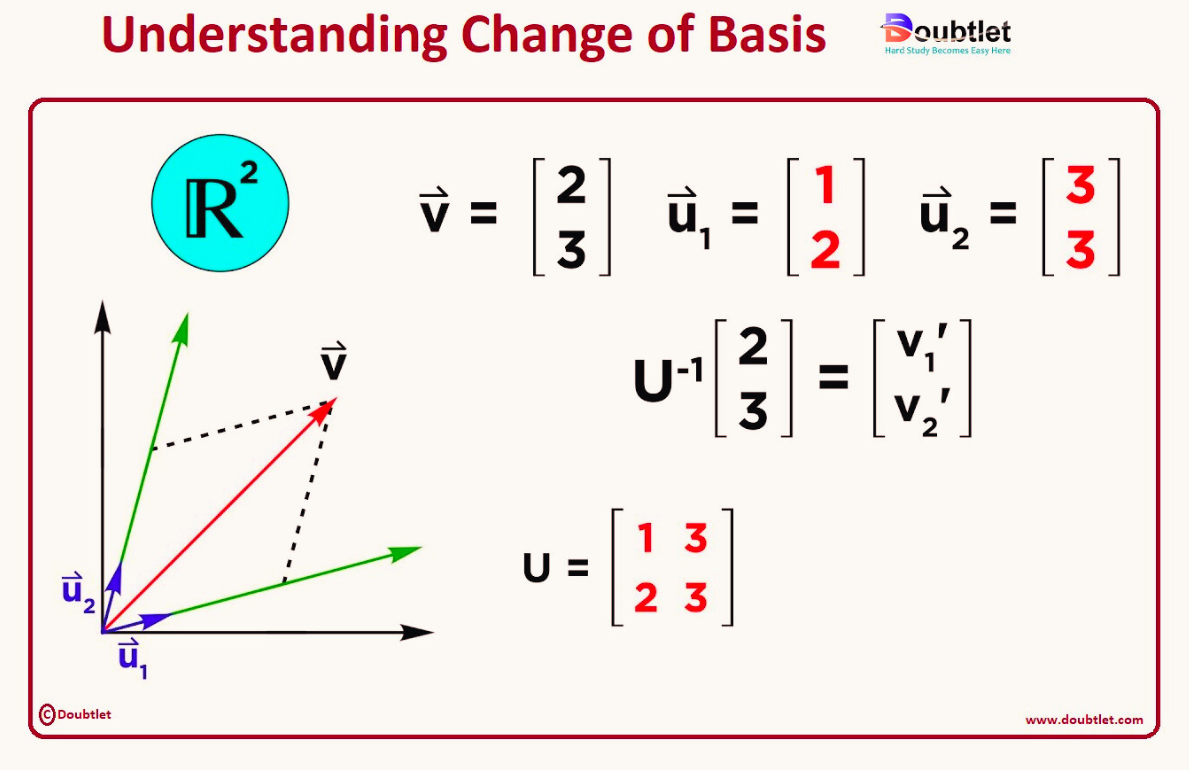
4. Why choose our Basis of a matrix Calculator?

$\bold{Easy \space \space to \space Use}$
Our calculator page provides a user-friendly interface that makes it accessible to both students and professionals. You can quickly input your square matrix and obtain the matrix of minors within a fraction of a second.

$\bold{Time \space Saving \space By \space automation}$
Our calculator saves you valuable time and effort. You no longer need to manually calculate each cofactor, making complex matrix operations more efficient.

$\bold{Accuracy \space and \space Precision}$
Our calculator ensures accurate results by performing calculations based on established mathematical formulas and algorithms. It eliminates the possibility of human error associated with manual calculations.

$\bold{Versatility}$
Our calculator can handle all input values like integers, fractions, or any real number.

$\bold{Complementary \space Resources}$
Alongside this calculator, our website offers additional calculators related to Pre-algebra, Algebra, Precalculus, Calculus, Coordinate geometry, Linear algebra, Chemistry, Physics, and various algebraic operations. These calculators can further enhance your understanding and proficiency.

5. A video based on the concept of how to find the Basis of a space spanned by the vectors.

6. How to use this calculator

This calculator will help you find the basis of a space spanned by vectors.
In the given input boxes, you have to put the value of the given vectors.
A step-by-step solution will be displayed on the screen after clicking the Calculate button.
You can access, download, and share the solution.

7. Solved Examples on Matrix Basis.

$\bold{Question}$
Find the basis of the space spanned by the vectors = {$\begin{bmatrix} 3 \\ 1 \\ 3 \end{bmatrix}$, $\begin{bmatrix} 2 \\ 7 \\ 5 \end{bmatrix}$, $\begin{bmatrix} 2 \\ 6 \\ 1 \end{bmatrix}$}
$\bold{Solution}$
$\bold{Step \space 1:}$ We can obtain the basis by finding row or column space.
$\bold{Step \space 2:}$ Row space is the basis of the vectors spanned = {$\begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}$, $\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}$, $\begin{bmatrix} 0\\ 0 \\ 1 \end{bmatrix}$}

8. Frequently Asked Questions (FAQs)

Why is the basis of a matrix important?

The basis provides a fundamental understanding of the vectors that define the matrix's space, playing a crucial role in various mathematical and real-world applications.

Can a matrix have multiple bases?

Yes, a matrix can have multiple bases. There are infinite ways to choose a set of linearly independent vectors that span its column space.

How do I find the basis of a matrix?

To find the basis, identify a set of linearly independent vectors that span the matrix's column space. These vectors form the basis.

What if the vectors are not linearly independent?

The vectors cannot form a basis if they are not linearly independent. In such cases, adjustments or transformations may be necessary.

Does the basis change if I scale the vectors?

Scaling the vectors does not change the basis. The basis remains the same as long as the vectors remain linearly independent and span the column space.

9. What are the real-life applications?

Understanding the basis of a matrix is vital in various fields, such as computer graphics, where matrices represent transformations. The basis vectors define the orientation and scale of objects in the graphical space.

The Matrix Basis Calculator is widely used in:

• Engineering: Structural analysis, physics simulations.
• Computer Science: Machine learning, graphics transformations.
• Data Science: Dimensionality reduction techniques (PCA).
• Cryptography: Basis selection for encryption algorithms.
• Physics: Quantum mechanics, relativity, and more.

Fictional Anecdote: Mark, a data scientist, used our calculator to reduce the dimensionality of a dataset before applying machine learning models, improving accuracy while reducing computation time.

10. Conclusion

As we conclude our exploration into the basis of a matrix, remember that it serves as the cornerstone for understanding the space encapsulated by matrices. Embrace the simplicity and significance of the basis and witness how it shapes our understanding of linear transformations in both mathematical realms and practical applications.

If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]

$\fcolorbox{black}{lightpink}{\color{blue}{Click here to Ask any Doubt}}$
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real time. Sign up and get registered with us.

$\color{red} \bold{Related \space Calculators}$

$\bold{Rank \space of \space a \space matrix}$
$\bold{Gram \space Schmidt \space Calculator}$
$\bold{Solving \space a \space system \space of \space linear \space equation}$
$\bold{Reduced \space row \space echelon \space form \space of \space a \space matrix}$
$\bold{Linear \space Independence \space of \space vectors}$
$\bold{Row \space space \space of \space a \space matrix}$
$\bold{Column \space space \space of \space a \space matrix}$