Compound Interest Calculator

Get Homework Help

Neetesh Kumar | February 7, 2025 $\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space$ Share this Page on:

Understanding how investments grow over time is essential when managing your finances. Whether you’re saving for retirement, planning a major purchase, or investing in your future, compound interest plays a critical role in how your money grows. The Compound Interest Calculator simplifies this process by helping you calculate the growth of your investment and understand the power of compounding.

In this blog post, we’ll explain what compound interest is, walk you through the formula, show you how to calculate it manually, and explore why our Compound Interest Calculator is the tool you need to make precise, fast, and accurate investment decisions.

1. Introduction to the Compound Interest Calculator

The Compound Interest Calculator helps you calculate how much interest you will earn on an investment or loan that compounds periodically. Unlike simple interest, where the interest is calculated only on the initial principal, compound interest allows the interest to be added to the principal at regular intervals, enabling your investment to grow exponentially over time.

The formula used in the calculator takes into account the initial principal, the interest rate, the time period, and the frequency of compounding, which can be daily, monthly, quarterly, or annually. Our calculator provides you with quick and accurate results, helping you track the growth of your investments or loans efficiently.

2. What is the Formulae used?

The Compound Interest Formula is:

$A = P \left( 1 + \dfrac{r}{n} \right)^{nt}$

Where:

• $A$ is the amount of money accumulated after interest (including principal).
• $P$ is the principal amount (the initial investment or loan amount).
• $r$ is the annual interest rate (in decimal form).
• $n$ is the number of times the interest is compounded per year.
• $t$ is the time the money is invested or borrowed for, in years.

This formula allows you to compute the final value of your investment or loan, factoring in the frequency of interest compounding.

3. How Do I Find the Compound Interest?

To calculate the compound interest, follow these steps:

Step 1: Identify Your Values

• Principal (P): The initial amount of money you invested or borrowed.
• Rate of Interest (r): The annual interest rate in decimal form.
• Number of Compounding Periods (n): The frequency of interest compounding per year (e.g., annually, quarterly, monthly).
• Time Period (t): The duration for which the money is invested or borrowed (in years).

Step 2: Apply the Compound Interest Formula

Plug the values into the formula:

$A = P \left( 1 + \dfrac{r}{n} \right)^{nt}$

This will give you the final amount $(A)$, which includes both the principal and the interest.

Step 3: Subtract the Principal to Find the Compound Interest

To find the compound interest itself, simply subtract the principal from the final amount:

$\text{Compound Interest} = A - P$

This will give you the interest earned over the investment period.

How to Calculate Compound Interest?

Let us understand the process of calculating compound interest with the help of the below example.

Example:

What amount is to be repaid on a loan of Rs. $12000$ for one and half years at $10\%$ per annum compounded half yearly?

Solution:

For the given situation, we can calculate the compound interest and total amount to be repaid on a loan in two ways. In the first method, we can directly substitute the values in the formula. In the second method, compound interest can be obtained by splitting the given time bound into equal periods.

Simple Interest: A Boring Story

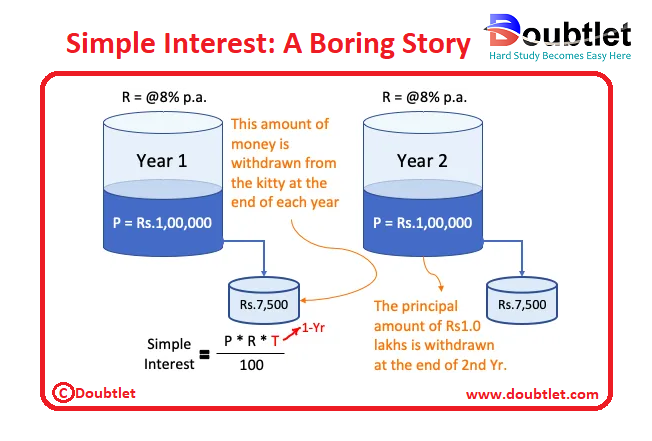
There was a person named Raj who received Rs. $1,00,000$ as a bonus from his employer. He wanted to spend the money on a later date. Hence, he decided to let it idle & generate some passive income from it.

He opened an FD in his bank and gave a standing instruction that, at the end of the year, the interest portion shall be credited in his savings account. Raj kept the FD live for $2$ years.

At the end of the first year, he got an interest income of Rs.$7,500$ (@$7.5\%$ on Rs.$1.0$ lakhs) credited to his savings account. The balance principal amount of Rs.$1.0$ lakhs was continued as FD. Similarly, at the end of the second year, he again got an interest income of Rs.$7,500$.

Please note that what Raj was earning on his deposit each year was simple interest.

What was the sum-total of this investment exercise? Principal plus first interest, plus the second interest $[\text{Rs}.(1,00,000 + 7500 + 7500) = 1,15,000]$. The passive income so generated was Rs.$15,000$ in two years.

The outcome of this FD could have been better than the above. How? By making the deposit earn compound interest instead of simple interest. What to do differently? To know this, let’s read another story.

Compound Interest: A Story

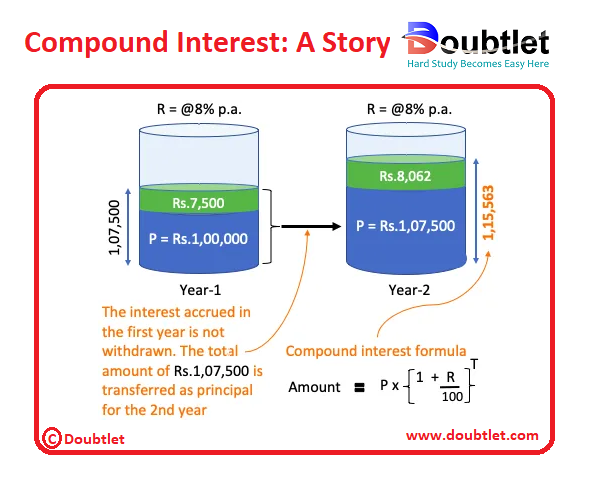
Raj received Rs.$1,00,000$ as a bonus from his employee. He wanted to use the money after $2$ years from now. Hence he decided to keep the money in a bank FD for the next $2$ years.

He opened an FD in his bank. He also gave a standing instruction to credit the principal amount and the accrued interest into his savings post maturity (after $2$ years).

In our simple interest story, even after the first year, the principal amount remained at Rs.$1,00,000$. Why? Because Raj withdrew the interest portion (Rs.$7,500$). But here, Raj allowed the interest to stay-put along with the principal amount. Hence, for year two, the principal amount became Rs.$107,500$. This amount then earned the interest @$7.5\%$ per annum at the end of the second year.

Just because Raj decided to let his money stay invested, he could take advantage of the power of compounding. In this story, Raj made Rs.$1,15,563$ at the end of the second year. This is more than what he made in story #1.

So what can we learn from these two stories? We will learn about a formula that highlights the parameters that we need to control in long-term investing. These controlling parameters can make us large amounts of money in times to come.

Benefits of Compound Interest

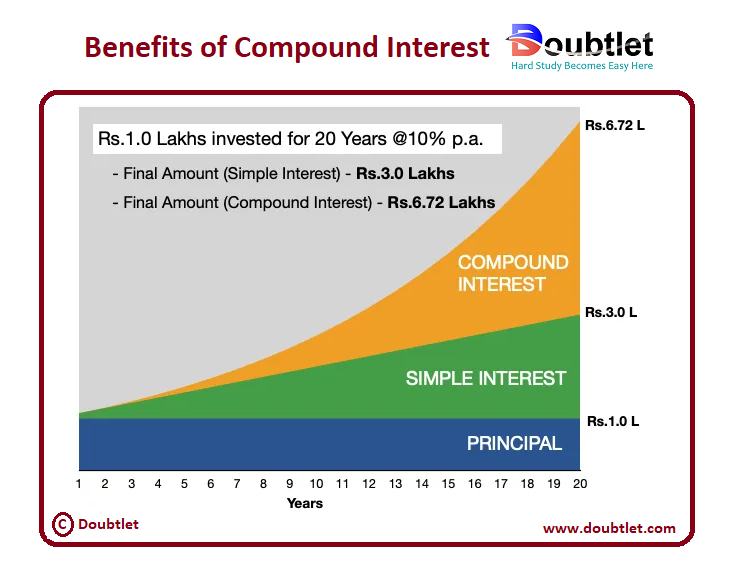
Allow me to give you another example of compound interest to see its benefits. In this example, we will again compare simple interest with compound interest.

Suppose you have Rs.$1.0$ Lakhs available for investing. You decided to invest this money in a hybrid mutual fund. This fund can yield $10\%$ p.a. return on average for the next $20$ years.

Had you not invested in a hybrid fund, and invested in an FD (say @$10\%$ p.a) paying-out annual income, you would be relying on simple interest. Using this route, your investment corpus would have become only Rs.$3.0$ lakhs after $20$ years (check this calculator).

A hybrid mutual fund, held for $20$ years, yielding a $10\%$ p.a. return would have increased your corpus from Rs.$1.0$ lakhs to Rs.$6.72$ lakhs in $20$ years (check this calculator).

To understand the effect of compounding more visually, we have provided a graph that draws a comparison between your initial investment, the final amount after simple-interest, and the final amount after compounding. Check the orange area to appreciate the benefit of compounding.

4. Why Choose Our Compound Interest Calculator?

$\bold{Easy \space \space to \space Use}$
Our calculator page provides a user-friendly interface that makes it accessible to both students and professionals. You can quickly input your square matrix and obtain the matrix of minors within a fraction of a second.

$\bold{Time \space Saving \space By \space automation}$
Our calculator saves you valuable time and effort. You no longer need to manually calculate each cofactor, making complex matrix operations more efficient.

$\bold{Accuracy \space and \space Precision}$
Our calculator ensures accurate results by performing calculations based on established mathematical formulas and algorithms. It eliminates the possibility of human error associated with manual calculations.

$\bold{Versatility}$
Our calculator can handle all input values like integers, fractions, or any real number.

$\bold{Complementary \space Resources}$
Alongside this calculator, our website offers additional calculators related to Pre-algebra, Algebra, Precalculus, Calculus, Coordinate geometry, Linear algebra, Chemistry, Physics, and various algebraic operations. These calculators can further enhance your understanding and proficiency.

5. A video based on how to Evaluate the Compound Interest.

6. How to use this calculator?

Using the Compound Interest Calculator is straightforward and quick:

1. Enter the Principal Amount: The initial amount of money you’ve invested or borrowed.
2. Enter the Interest Rate: The annual interest rate in decimal form (e.g., $5\%$ as $0.05$).
3. Choose the Compounding Frequency: Select whether the interest is compounded annually, quarterly, monthly, or daily.
4. Enter the Time Period: The duration (in years) for which you want to calculate the compound interest.
5. Click Calculate: Get your results in an instant!

The calculator will show you the final amount and the interest earned over the period.

7. Solved Examples on Compound Interest.

Example 1: Annual Compounding

You invest $1,000$ at an annual interest rate of $5\%$, compounded annually for $3$ years.

Using the compound interest formula:

Solutions:

$A = 1000 \left( 1 + \dfrac{0.05}{1} \right)^3 = 1000 \times (1.05)^3 = 1000 \times 1.157625 = 1157.63$

The final amount is $1,157.63$, and the compound interest earned is:

$1157.63 - 1000 = 157.63$

Example 2: Monthly Compounding

You invest $500$ at an annual interest rate of $6\%$, compounded monthly for $5$ years.

Using the formula:

Solutions:

$A = 500 \left( 1 + \dfrac{0.06}{12} \right)^{12 \times 5} = 500 \times (1 + 0.005)^{60} = 500 \times (1.005)^{60} = 500 \times 1.34885 = 674.42$

The final amount is $674.42$, and the compound interest earned is:

$674.42 - 500 = 174.42$

8. Frequently Asked Questions (FAQs)

Q1. What is compound interest?

Compound interest is the interest calculated on both the initial principal and the accumulated interest from previous periods.

Q2. How is compound interest different from simple interest?

Simple interest is calculated only on the initial principal, while compound interest is calculated on both the principal and the accumulated interest.

Q3. What are the different compounding frequencies?

Compounding can be done annually, quarterly, monthly, or daily, affecting how often interest is added to the principal.

Q4. Can I use this calculator for loans?

Yes, the calculator works for both investments and loans to help you understand how compound interest impacts your finances.

Q5. How do I convert the interest rate into decimal form?

To convert the interest rate from percentage to decimal, simply divide by $100$ (e.g., $6\%$ becomes $0.06$).

Q6. Can I use this for long-term investments?

Yes, the calculator is designed to work for any time period, whether short-term or long-term investments.

Q7. How accurate is this calculator?

The calculator is highly accurate, performing the complex mathematical calculations in an instant.

Q8. Is this tool free?

Yes, our Compound Interest Calculator is completely free to use.

9. What Are the Real-Life Applications?

Compound interest is used in many real-life financial scenarios:

• Savings accounts: Growing your money with interest over time.
• Investments: Calculating the return on stocks, bonds, and mutual funds.
• Loans: Understanding how interest accrues on student loans, mortgages, and credit cards.
• Retirement planning: Estimating the growth of your retirement savings.
• Financial planning: Forecasting future value for investments and goals.

10. Conclusion

The Compound Interest Calculator is a powerful and essential tool for anyone looking to manage their finances or investments. It simplifies the complex process of calculating compound interest and allows you to make more informed decisions about saving, investing, or borrowing money.

Ready to see how compound interest works for you? Try our calculator today and experience the power of compound growth!

If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]

$\fcolorbox{black}{lightpink}{\color{blue}{Click here to Ask any Doubt}}$
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real time. Sign up and get registered with us.

$\color{red} \bold{Related \space Calculators}$
8th Pay Commission Salary Calculator
Age Calculator
Simple Interest Calculator
Space Travel Cost Calculator
Weight on Mars Calculator
Degree and Leading Coefficient Calculator
Nth Root calculator