Derivative Calculator

Get Homework Help

In the world of calculus, derivatives are everywhere from tracking the speed of a moving car to modeling changes in economics or physics. But let’s face it manually finding derivatives can get messy, especially when you're knee-deep in exponents, chains, and product rules.

That’s why our Derivative Calculator exists: to simplify your life. Whether you're a student, teacher, engineer, or data scientist, this tool quickly and accurately computes derivatives of any function.

1. Introduction to the Derivative Calculator

Our Derivative Calculator is an intelligent online tool designed to help you compute the derivative of any function be it algebraic, trigonometric, exponential, or logarithmic. Whether you're building a study guide or tackling complex real-world equations, this calculator gets you from input to answer in a blink.

What makes it table-friendly? It doesn't just give one result it shows derivatives step-by-step, supports tabular comparisons, and lets you see first, second, or higher-order derivatives all in one go.

2. What is the Formulae used?

The derivative of a function measures how the function’s output changes as its input changes. The most basic definition is:

$f'(x) = \displaystyle\lim_{h \to 0} \frac{f(x + h) - f(x)}{h}$

This is called the limit definition of a derivative. However, when you're working through real problems, you’ll likely use these common rules:

• Power Rule:

$\dfrac{d}{dx} \left( x^n \right) = n x^{n - 1}$

• Product Rule:

$\dfrac{d}{dx} \left[ u(x)v(x) \right] = u'(x)v(x) + u(x)v'(x)$

• Quotient Rule:

$\dfrac{d}{dx} \left[ \dfrac{u(x)}{v(x)} \right] = \dfrac{u'(x)v(x) - u(x)v'(x)}{[v(x)]^2}$

• Chain Rule:

$\dfrac{d}{dx} \left[ f(g(x)) \right] = f'(g(x)) \cdot g'(x)$

Our Derivative Calculator uses these formulas under the hood to process derivatives of complex and composite functions efficiently.

3. How Do I Find the Derivative?

Finding a derivative typically involves:

1. Identifying the function: Determine what you're differentiating.
2. Choosing the rule: Use power, chain, product, or quotient rule depending on the function.
3. Applying the rule correctly: Carefully differentiate each term.
4. Simplifying the result: Clean up the expression for clarity.

Or... you could just plug it into our calculator and let it do the heavy lifting for you.

4. Why Choose Our Derivative Calculator?

$\bold{Easy \space \space to \space Use}$
Our calculator page provides a user-friendly interface that makes it accessible to both students and professionals. You can quickly input your square matrix and obtain the matrix of minors within a fraction of a second.

$\bold{Time \space Saving \space By \space automation}$
Our calculator saves you valuable time and effort. You no longer need to manually calculate each cofactor, making complex matrix operations more efficient.

$\bold{Accuracy \space and \space Precision}$
Our calculator ensures accurate results by performing calculations based on established mathematical formulas and algorithms. It eliminates the possibility of human error associated with manual calculations.

$\bold{Versatility}$
Our calculator can handle all input values like integers, fractions, or any real number.

$\bold{Complementary \space Resources}$
Alongside this calculator, our website offers additional calculators related to Pre-algebra, Algebra, Precalculus, Calculus, Coordinate geometry, Linear algebra, Chemistry, Physics, and various algebraic operations. These calculators can further enhance your understanding and proficiency.

5. A video based on how to Evaluate the Derivative.

6. How to use this calculator?

It’s super straightforward:

1. Enter your function in the input field (e.g., $x^2 + 3x - \sin(x)$).
2. Select the order of derivative (1st, 2nd, or higher).
3. Choose the variable to differentiate with respect to ($x$, $t$, $y$, etc.).
4. Click "Calculate".
5. View the output, including step-by-step breakdowns and simplified results.

Boom. Math done in seconds.

7. Solved Examples on Derivative.

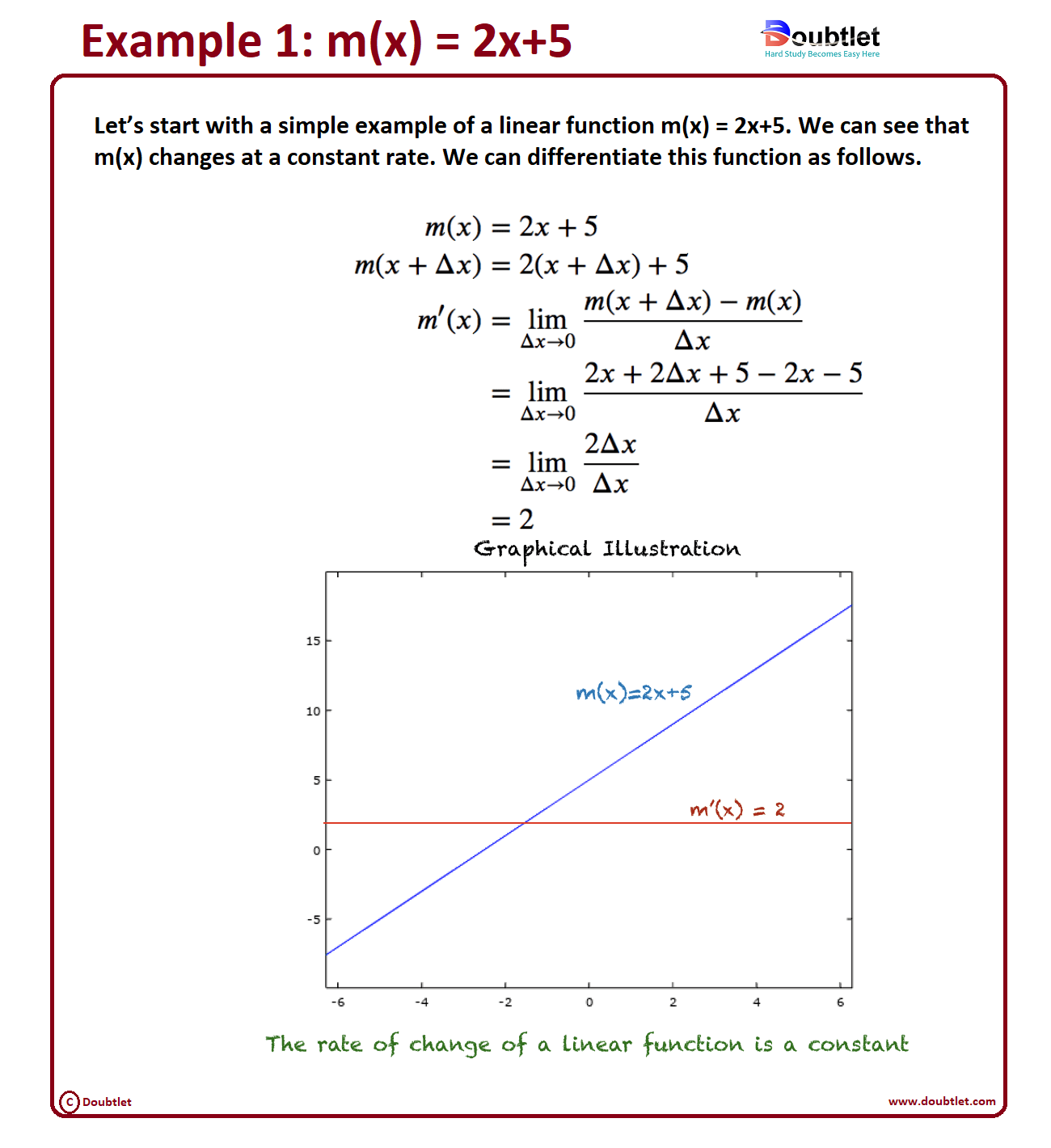
Example 1: Basic Polynomial

Function:

$f(x) = x^3 + 5x^2 - 4x + 7$

Solutons:

Derivative:

$\dfrac{d}{dx} \left[ x^3 + 5x^2 - 4x + 7 \right]$

$= \dfrac{d}{dx} \left[ x^3 \right] + 5 \cdot \frac{d}{dx} \left[ x^2 \right] - 4 \cdot \frac{d}{dx} \left[ x \right] + \frac{d}{dx} \left[ 7 \right]$

$= 3x^2 + 5 \cdot 2x - 4 \cdot 1 + 0$

$= 3x^2 + 10x - 4$

Answer: $f'(x) = \boxed{3x^2 + 10x - 4}$

Example 2: Trigonometric Function

Function:

$f(x) = \sin(x) \cdot \cos(x)$

Solutons:

Derivative (using the product rule):

$\dfrac{d}{dx} \left[ \cos(x) \cdot \sin(x) \right]$

$= \dfrac{d}{dx} \left[ \cos(x) \right] \cdot \sin(x) + \cos(x) \cdot \frac{d}{dx} \left[ \sin(x) \right]$

$= (-\sin(x)) \sin(x) + \cos(x) \cos(x)$

$= \cos^2(x) - \sin^2(x)$

Answer: $f'(x) = \boxed{\cos^2(x) - \sin^2(x)}$

Example 3: Exponential with Chain Rule

Function:

$f(x) = e^{x^2}$

Solutons:

Derivative:

$\dfrac{d}{dx} \left[ e^{x^2} \right]$

$= e^{x^2} \cdot \frac{d}{dx} \left[ x^2 \right]$

$= e^{x^2} \cdot 2x$

$= 2x e^{x^2}$

Answer: $f'(x) = \boxed{2xe^{x^2}}$

Use our calculator to verify or expand more complex examples like these instantly!

8. Frequently Asked Questions (FAQs)

Q1. Can this calculator solve higher-order derivatives?

Yes! You can compute the first, second, third, or even nth derivative.

Q2. Does it support trigonometric and logarithmic functions?

Absolutely. It handles $\sin(x), \cos(x), \tan(x), \ln(x), \log(x)$, and more.

Q3. Is there a limit to the function length?

Technically no, but extremely long expressions may take longer to process.

Q4. Can I input parametric equations?

Currently, we support single-variable functions. Parametric support is on the roadmap.

Q5. Is this calculator accurate?

It uses standard differentiation rules and symbolic math engines, ensuring highly accurate results.

Q6. Do I need to install anything?

Nope. It runs entirely in your browser.

Q7. Can I export the results?

Yes, results can be copied and pasted into documents or tables for easy use.

Q8. Is this tool free forever?

Yes! We believe powerful math tools should be accessible to everyone.

9. What Are the Real-Life Applications?

The concept of a derivative isn’t just academic. It’s used everywhere:

• Economics – To find marginal cost and revenue
• Physics – To compute velocity and acceleration
• Biology & Medicine – In modeling population growth and rates of change
• AI & Machine Learning – During optimization in backpropagation
• Data Analytics – To analyze trends and inflection points

In short, derivatives help describe how things change, making them vital in every data-driven or science-based field.

10. Conclusion

If you’re dealing with calculus, derivatives are unavoidable. But the math doesn’t have to slow you down.
Our Derivative Calculator helps you compute answers accurately, quickly, and stress-free.

Whether you’re solving a homework problem, debugging a formula, or analyzing change in a dataset — this tool has your back.

Try the Derivative Calculator now and turn complex functions into clean, step-by-step answers in seconds!

---

If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]

$\fcolorbox{black}{lightpink}{\color{blue}{Click here to Ask any Doubt}}$
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real time. Sign up and get registered with us.

$\color{red} \bold{Related \space Calculators}$
Simpson’s one third Rule for a Table Calculator
Simpson’s three by eight rule for a table Calculator
Harmonic Mean Calculator
Percentile Calculator
Mode Calculator
Median Calculator
Lower Quartile Calculator
Chain Rule in Derivatives Blog
Derivatives and Integrals Cheat Sheet