FOIL Method Calculator

Get Homework Help

Neetesh Kumar | January 20, 2024 $\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space$ Share this Page on:

The FOIL Method is a simple and effective way to multiply binomials, a crucial concept in algebra. The FOIL Method Calculator for a Table streamlines this process, enabling students, educators, and professionals to solve problems quickly and accurately. Whether you’re working on algebraic expressions or preparing for exams, this calculator is your ultimate solution.

1. Introduction to the FOIL Method Calculator

The FOIL Method stands for First, Outer, Inner, and Last, representing the steps to multiply two binomials. This method ensures that every term is accounted for, making it an essential tool in algebra.

Our FOIL Method Calculator is designed for efficiency, especially when dealing with multiple problems or tabular data. Simply input your binomials, and the calculator will do the rest, saving time and reducing errors.

2. What is the Formulae used?

The FOIL Method involves multiplying two binomials, $(a + b)(c + d)$, by following these steps:

1. First: Multiply the first terms of each binomial. $a \cdot c$

2. Outer: Multiply the outer terms. $a \cdot d$

3. Inner: Multiply the inner terms. $b \cdot c$

4. Last: Multiply the last terms of each binomial. $b \cdot d$

Combine all these products:

$(a + b)(c + d) = ac + ad + bc + bd$

The result is a trinomial or a polynomial depending on the coefficients.

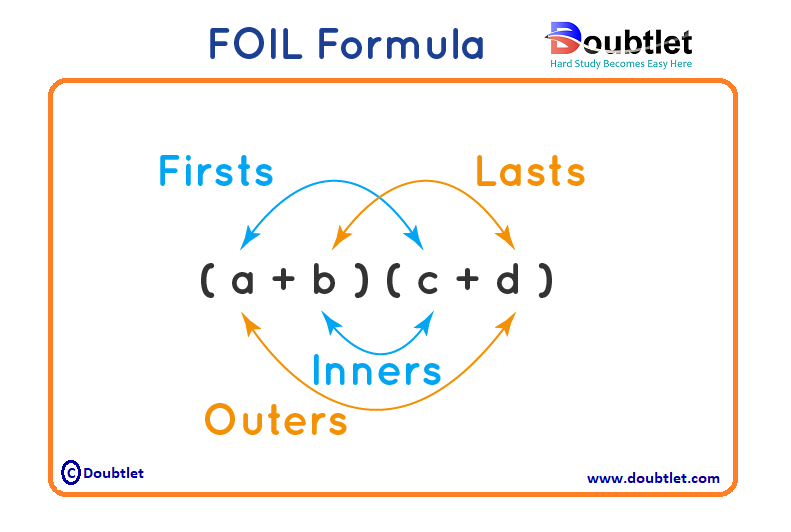
3. How Do I Find the FOIL Method?

To use the FOIL Method manually:

1. Write Down the Binomials: For example, $(x^2 + 3)(x - 2)$.

2. Apply FOIL: Multiply:

   • First: $x^2 \cdot x = x^3$.
   • Outer: $x^2 \cdot -2 = -2x^2$.
   • Inner: $3 \cdot x = 3x$.
   • Last: $3 \cdot -2 = -6$.

3. Combine Like Terms: $x^3 - 2x^2 + 3x - 6 = x^3 - 2x^2 + 3x - 6$

Our calculator automates this process, especially for multiple binomials or complex expressions.

How to FOIL

The mnemonic FOIL tells us precisely what terms to multiply and in what order:

• First – multiply the first terms.
• Outside – multiply the outside/outer terms.
• Inside – multiply the inside/inner terms.
• Last – multiply the last terms.

By following First, Outer, Inner, Last, we do not overlook any term in either binomial. All the terms in the first binomial are combined with the terms in the second binomial properly. Everything gets counted.

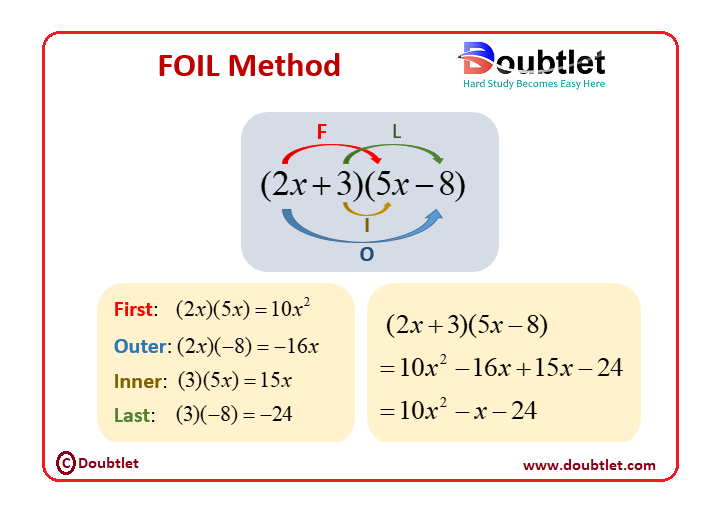
Understanding the FOIL Method

The FOIL Method is a technique used to multiply two binomials. FOIL stands for:

• F: First terms,
• O: Outer terms,
• I: Inner terms,
• L: Last terms.

For two binomials, $(a + b)$ and $(c + d)$, the product is:

$(a + b)(c + d) = ac + ad + bc + bd$

Steps to Apply the FOIL Method

1. Multiply the First terms.
2. Multiply the Outer terms.
3. Multiply the Inner terms.
4. Multiply the Last terms.
5. Combine like terms (if applicable).

Solved Examples

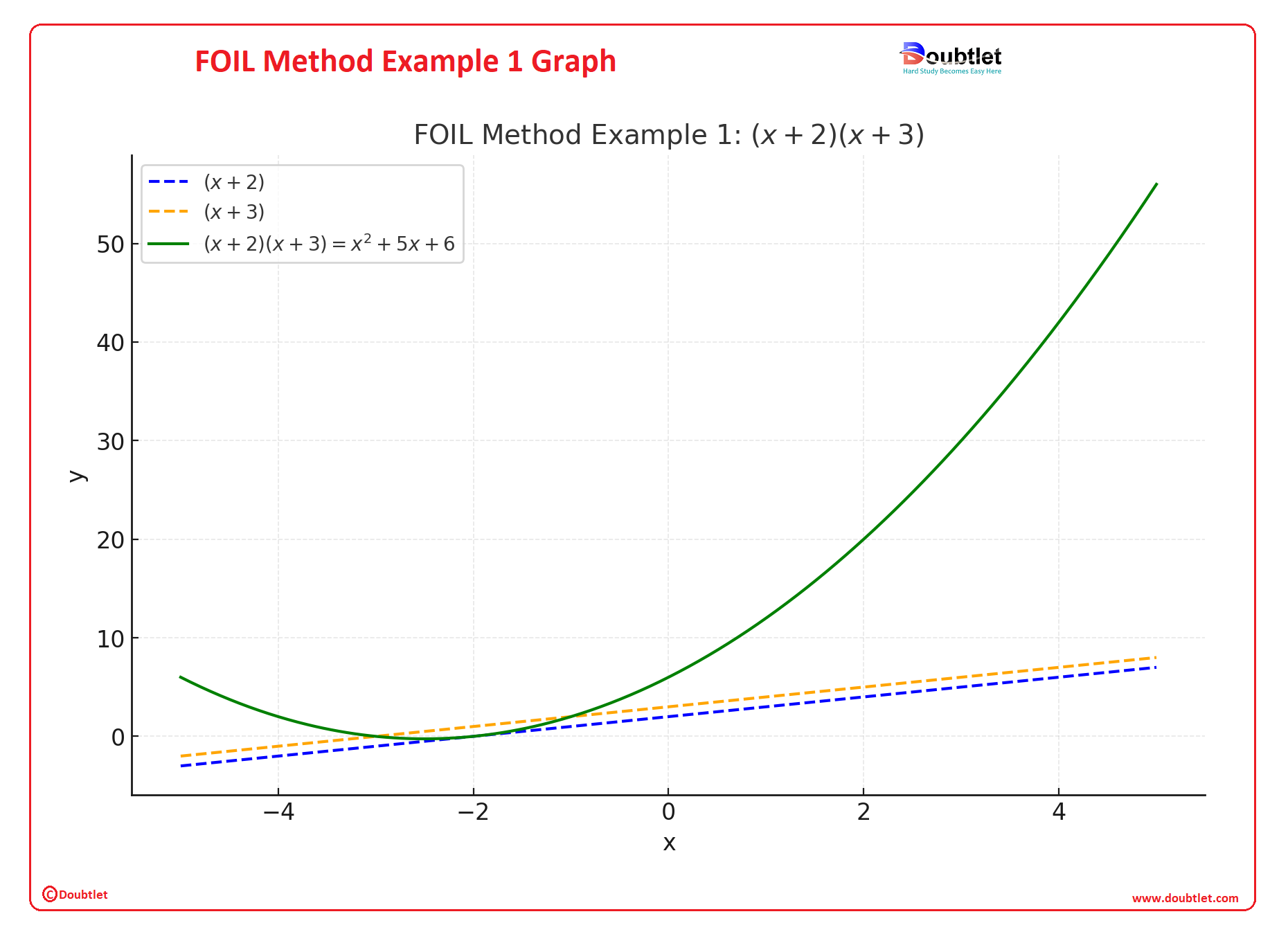
Example 1: Multiply $(x + 2)(x + 3)$

Solutions:

1. First terms: $x \cdot x = x^2$,
2. Outer terms: $x \cdot 3 = 3x$,
3. Inner terms: $2 \cdot x = 2x$,
4. Last terms: $2 \cdot 3 = 6$.

Combine the results:

$x^2 + 3x + 2x + 6 = x^2 + 5x + 6$

Answer:

$(x + 2)(x + 3) = x^2 + 5x + 6$

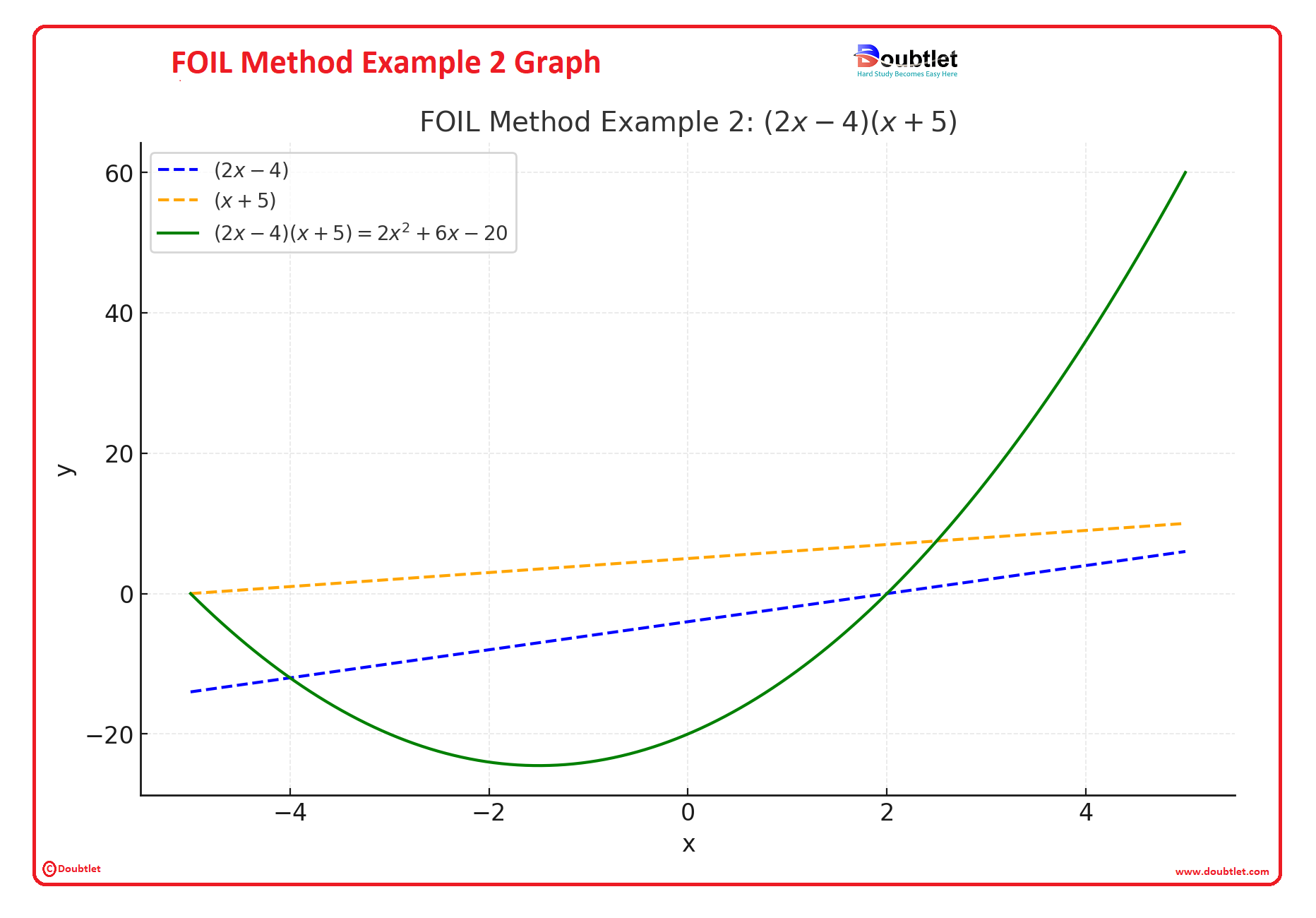
Example 2: Multiply $(2x - 4)(x + 5)$

Solutions:

1. First terms: $2x \cdot x = 2x^2$,
2. Outer terms: $2x \cdot 5 = 10x$,
3. Inner terms: $-4 \cdot x = -4x$,
4. Last terms: $-4 \cdot 5 = -20$.

Combine the results:

$2x^2 + 10x - 4x - 20 = 2x^2 + 6x - 20$

Answer:

$(2x - 4)(x + 5) = 2x^2 + 6x - 20$

Example 3: Multiply $(x + 1)(x - 1)$

Solutions:

1. First terms: $x \cdot x = x^2$,
2. Outer terms: $x \cdot -1 = -x$,
3. Inner terms: $1 \cdot x = x$,
4. Last terms: $1 \cdot -1 = -1$.

Combine the results:

$x^2 - x + x - 1 = x^2 - 1$

Answer:

$(x + 1)(x - 1) = x^2 - 1$

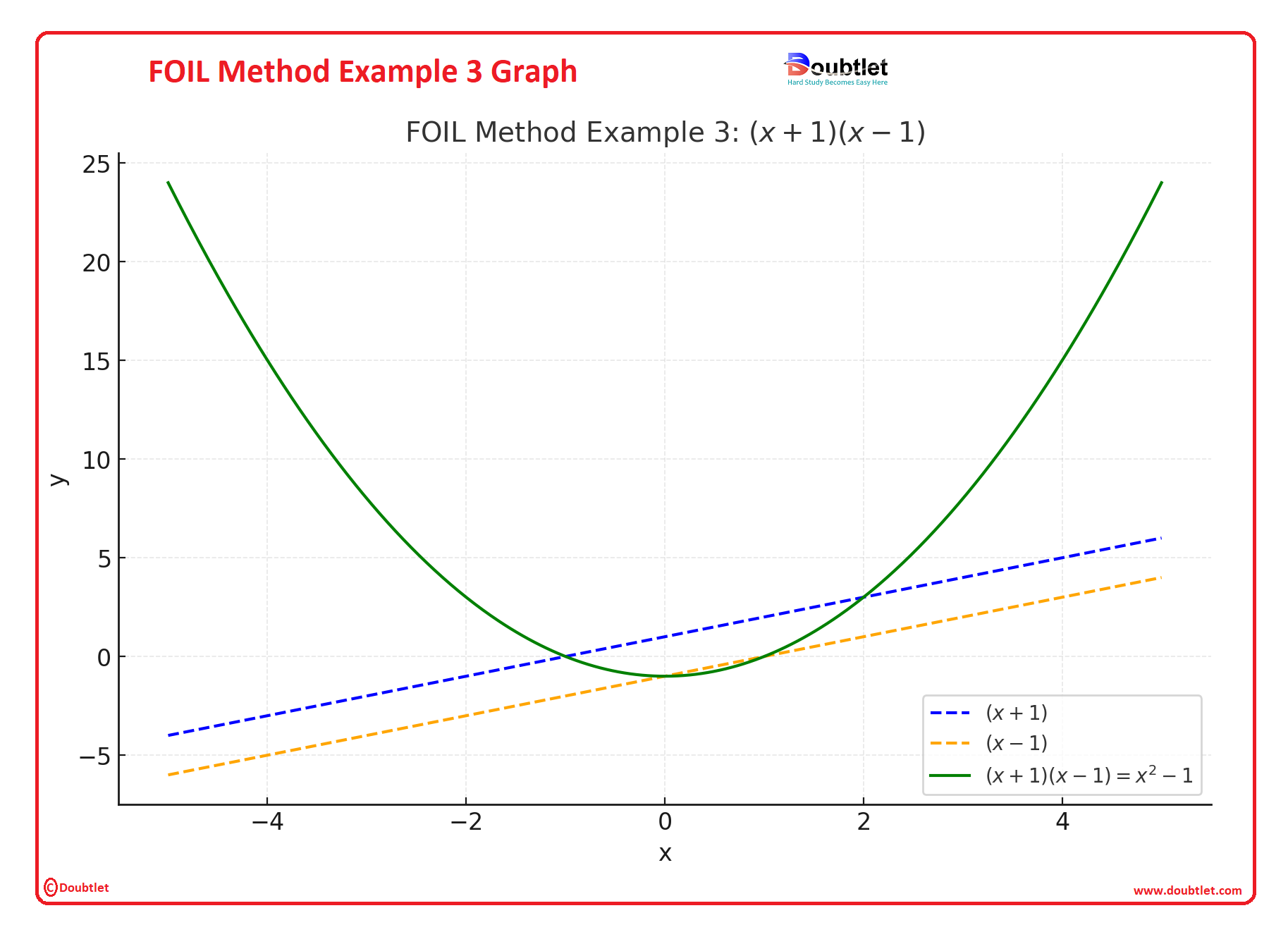
Explanation of the Graphs:

1. Example 1 $((x + 2)(x + 3))$:

   • The blue and orange dashed lines represent the binomials $(x + 2)$ and $(x + 3)$, respectively.
   • The green curve shows the product of the binomials, $(x + 2)(x + 3) = x^2 + 5x + 6$.

2. Example 2 $((2x - 4)(x + 5))$:

   • The blue dashed line represents $(2x - 4)$, and the orange dashed line represents $(x + 5)$.
   • The green curve represents the product, $(2x - 4)(x + 5) = 2x^2 + 6x - 20$.

3. Example 3 $((x + 1)(x - 1))$:

   • The blue dashed line is $(x + 1)$, and the orange dashed line is $(x - 1)$.
   • The green curve is the product, $(x + 1)(x - 1) = x^2 - 1$.

Key Insights:

• The graphs visually demonstrate how the product of two binomials forms a parabola (quadratic equation).
• The intersections and relative shapes of the curves help verify the correctness of the FOIL method.

4. Why Choose Our FOIL Method Calculator?

$\bold{Easy \space \space to \space Use}$
Our calculator page provides a user-friendly interface that makes it accessible to both students and professionals. You can quickly input your square matrix and obtain the matrix of minors within a fraction of a second.

$\bold{Time \space Saving \space By \space automation}$
Our calculator saves you valuable time and effort. You no longer need to manually calculate each cofactor, making complex matrix operations more efficient.

$\bold{Accuracy \space and \space Precision}$
Our calculator ensures accurate results by performing calculations based on established mathematical formulas and algorithms. It eliminates the possibility of human error associated with manual calculations.

$\bold{Versatility}$
Our calculator can handle all input values like integers, fractions, or any real number.

$\bold{Complementary \space Resources}$
Alongside this calculator, our website offers additional calculators related to Pre-algebra, Algebra, Precalculus, Calculus, Coordinate geometry, Linear algebra, Chemistry, Physics, and various algebraic operations. These calculators can further enhance your understanding and proficiency.

5. A video based on how to Evaluate the FOIL Method.

6. How to use this calculator?

Using the FOIL Method Calculator is simple:

1. Input the Binomials: Enter the expressions in the provided fields or upload a table.

2. Click Calculate: Instantly view the expanded polynomial.

3. Analyze Results: Use the output for graphing, further calculations, or homework checks.

This tool ensures accurate and efficient solutions for all your binomial multiplication needs.

7. Solved Examples on FOIL Method

Example 1:

Multiply $(x + 4)(x - 2)$:

Solution:

1. First: $x \cdot x = x^2$.

2. Outer: $x \cdot -2 = -2x$.

3. Inner: $4 \cdot x = 4x$.

4. Last: $4 \cdot -2 = -8$.

5. Combine: $x^2 - 2x + 4x - 8 = x^2 + 2x - 8$

Example 2: Tabular Data:

Steps:

1. Input the binomials into the calculator..

2. Compute the expanded polynomial for each pair.

8. Frequently Asked Questions (FAQs)

Q1. What is the FOIL Method?

The FOIL Method is a technique to multiply two binomials by focusing on First, Outer, Inner, and Last terms.

Q2. Is it only for binomials?

Yes, the FOIL Method specifically applies to binomial multiplication.

Q3. Can this calculator handle large datasets?

Yes, it’s designed for tabular data and bulk processing.

Q4. Is this calculator free?

Yes, our FOIL Method Calculator is completely free to use.

Q5. Does it work for non-linear expressions?

The calculator is optimized for binomial expressions but can handle polynomial expansions as well.

Q6. Is the calculator mobile-friendly?

Absolutely, it works seamlessly on any device.

Q7. Can I export the results?

Yes, you can download the outputs for further analysis or documentation.

Q8. Does it show intermediate steps?

Yes, detailed calculations are displayed for better understanding.

9. What are the real-life applications?

The FOIL Method is widely used in:

• Algebra: Solve quadratic equations and simplify expressions.
• Engineering: Analyze polynomial functions in systems.
• Physics: Model motion and forces.
• Economics: Represent cost functions and revenue models.
• Education: Teach and learn algebraic multiplication.

Fictional Anecdote: Emily, a high school math teacher, uses our FOIL Method Calculator to create problem sets for her students. With quick results, she spends more time explaining concepts and less on manual calculations.

10. Conclusion

The FOIL Method Calculator is a powerful tool for simplifying algebraic multiplication. It saves time, ensures accuracy, and supports tabular data, making it ideal for students, educators, and professionals.

Ready to simplify polynomial multiplication? Try our FOIL Method Calculator today and unlock the ease of accurate algebraic solutions!

If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]

$\fcolorbox{black}{lightpink}{\color{blue}{Click here to Ask any Doubt}}$
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real time. Sign up and get registered with us.

$\color{red} \bold{Related \space Calculators}$
Laplace Transform Calculator
X and Y Intercepts Calculator
Fraction to Percent Calculator
Logarithm Calculator
Cube Root Calculator
Exponential Function Calculator
BMI Calculator