Laplace Transform Calculator

Get Homework Help

Neetesh Kumar | January 27, 2025 $\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space$ Share this Page on:

The Laplace Transform Calculator is an invaluable tool for solving complex differential equations and analyzing systems in various fields like engineering, physics, and mathematics. Whether you're a student tackling tough problems or a professional working on advanced computations, this calculator ensures accurate results and simplifies the process. With support for individual functions and tabular datasets, it caters to all your mathematical needs efficiently.

1. Introduction to the Laplace Transform Calculator

The Laplace Transform is a mathematical operation that converts a time-domain function into a complex frequency-domain representation. This transformation is widely used to simplify differential equations, analyze system dynamics, and solve real-world problems in engineering and science.

Our Laplace Transform Calculator for a Table is designed to handle individual and bulk data inputs, making it perfect for classrooms, research labs, and professional projects.

2. What is the Formulae used?

Laplace Transform Definition

The Laplace Transform of a function $f(t)$ is defined as:

$\mathcal{L}\{f(t)\} = F(s) = \displaystyle\int_{0}^{\infty} e^{-st} f(t) \, dt$

Where:

• $\mathcal{L}\{f(t)\}$: Laplace Transform of $f(t)$.
• $F(s)$: Transformed function in the $s$-domain.
• $t$: Time-domain variable.
• $s$: Complex frequency variable.

Common Laplace Transform Pairs

1. $f(t) = 1$: $F(s) = \dfrac{1}{s}$

   
   

2. $f(t) = e^{at}$: $F(s) = \dfrac{1}{s-a}$

   
   

3. $f(t) = \sin(at)$: $F(s) = \dfrac{a}{s^2 + a^2}$

   
   

4. $f(t) = \cos(at)$: $F(s) = \dfrac{s}{s^2 + a^2}$

3. How Do I Find the Laplace Transform?

To Compute the Laplace Transform Manually:

1. Identify $f(t)$: Start with the given time-domain function.
2. Apply the Formula: Substitute $f(t)$ into $\displaystyle\int_{0}^{\infty} e^{-st} f(t) \, dt$.
3. Simplify the Integral: Solve the integral step by step.
4. Express in Terms of $s$: Write the transformed function $F(s)$.

Example:

Find the Laplace Transform of $f(t) = e^{3t}$:

1. Formula:

   $\mathcal{L}\{e^{3t}\} = \displaystyle\int_{0}^{\infty} e^{-st} e^{3t} \, dt$

2. Simplify:

   $\displaystyle\int_{0}^{\infty} e^{(3-s)t} \, dt = \frac{1}{s - 3} \quad \text{for } s > 3$

3. Result:

   $\mathcal{L}\{e^{3t}\} = \dfrac{1}{s - 3}$

Our calculator automates this process for both standard and custom functions, saving time and effort.

Understanding the Laplace Transform

The Laplace Transform converts a time-domain function $f(t)$ into a frequency-domain function $F(s)$. It is defined as:

$\mathcal{L}\{f(t)\} = F(s) = \displaystyle\int_{0}^{\infty} f(t) e^{-st} dt$

Where:

• $f(t)$: Time-domain function,
• $F(s)$: Laplace transform in the $s$-domain,
• $s$: Complex frequency variable.

Example 1: Laplace Transform of a Constant Function

Problem: Find the Laplace transform of $f(t)=1$.

Solution:

Solving the Laplace Transform for $f(t) = 1$

1. Definition of the Laplace Transform:

   $\mathcal{L}\{1\} = \displaystyle\int_{0}^{\infty} 1 \cdot e^{-st} dt$

2. Evaluate the Integral:

   $\mathcal{L}\{1\} = \displaystyle\int_{0}^{\infty} e^{-st} dt$

   The integral of $e^{-st}$ is:

   $\displaystyle\int e^{-st} dt = \frac{e^{-st}}{-s}$

3. Apply the Limits:

   $\mathcal{L}\{1\} = \left[ \frac{e^{-st}}{-s} \right]_{0}^{\infty}$

   • At $t = \infty$, $e^{-st} \to 0$ (for $s > 0$).
   • At $t = 0$, $e^{-st} = 1$.

   Substituting the limits:

   $\mathcal{L}\{1\} = \dfrac{0 - 1}{-s} = \dfrac{1}{s}$

Answer:

$\mathcal{L}\{1\} = \dfrac{1}{s}, \quad s > 0$

Example 2: Laplace Transform of $f(t) = e^{at}$

Problem: Find the Laplace Transform of $f(t) = e^{at}$.

Solution:

1. Definition:

   $\mathcal{L}\{e^{at}\} = \displaystyle\int_{0}^{\infty} e^{at} e^{-st} dt = \int_{0}^{\infty} e^{-(s-a)t} dt$

2. Evaluate the Integral:

   $\displaystyle\int_{0}^{\infty} e^{-(s-a)t} dt = \frac{e^{-(s-a)t}}{-(s-a)}$

3. Apply the Limits:

   $\mathcal{L}\{e^{at}\} = \left[ \dfrac{e^{-(s-a)t}}{-(s-a)} \right]_{0}^{\infty}$

   • At $t = \infty$, $e^{-(s-a)t} \to 0$ (if $s > a$).
   • At $t = 0$, $e^{-(s-a)t} = 1$.

   Substituting the limits:

   $\mathcal{L}\{e^{at}\} = \dfrac{0 - 1}{-(s-a)} = \dfrac{1}{s-a}$

Answer:

$\mathcal{L}\{e^{at}\} = \dfrac{1}{s-a}, \quad s > a$

Graph Explanation

Let’s visualize the time-domain functions $f(t)=1$ and $f(t)=e^{at}$ alongside their Laplace transforms.

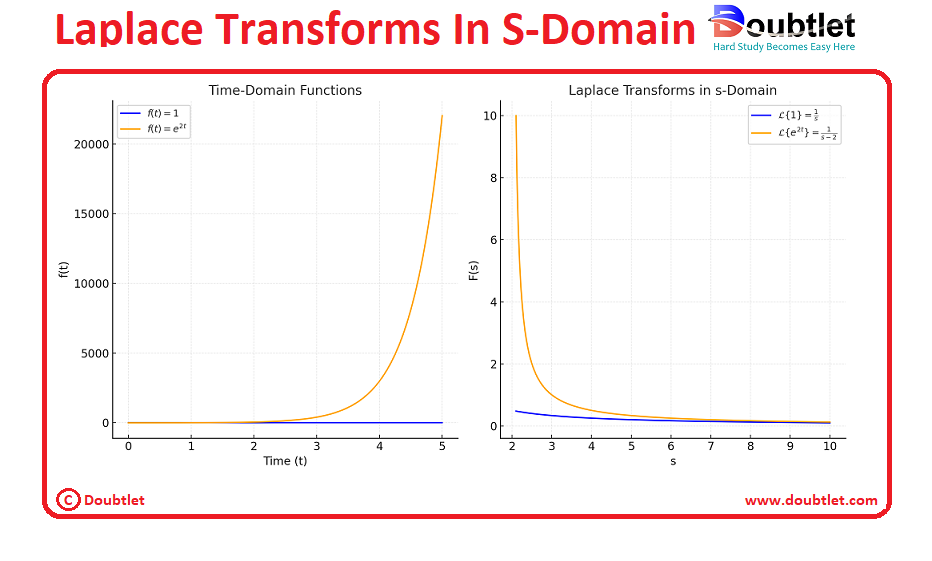
Explanation of the Graphs:

1. Time-Domain Functions:

   • The blue line represents $f(t) = 1$, which is constant over time.
   • The orange curve represents $f(t) = e^{2t}$, which grows exponentially as time increases.

2. Laplace Transforms in the $s$-Domain:

   • The blue curve shows $\mathcal{L}\{1\} = \dfrac{1}{s}$, which decreases as $s$ increases.
   • The orange curve shows $\mathcal{L}\{e^{2t}\} = \dfrac{1}{s - 2}$, which is only valid for $s > 2$.

3. Key Insight:

   • The Laplace transform converts time-domain functions into the $s$-domain, simplifying the analysis of systems, especially in engineering and differential equations.

4. Why Choose Our Laplace Transform Calculator?

$\bold{Easy \space \space to \space Use}$
Our calculator page provides a user-friendly interface that makes it accessible to both students and professionals. You can quickly input your square matrix and obtain the matrix of minors within a fraction of a second.

$\bold{Time \space Saving \space By \space automation}$
Our calculator saves you valuable time and effort. You no longer need to manually calculate each cofactor, making complex matrix operations more efficient.

$\bold{Accuracy \space and \space Precision}$
Our calculator ensures accurate results by performing calculations based on established mathematical formulas and algorithms. It eliminates the possibility of human error associated with manual calculations.

$\bold{Versatility}$
Our calculator can handle all input values like integers, fractions, or any real number.

$\bold{Complementary \space Resources}$
Alongside this calculator, our website offers additional calculators related to Pre-algebra, Algebra, Precalculus, Calculus, Coordinate geometry, Linear algebra, Chemistry, Physics, and various algebraic operations. These calculators can further enhance your understanding and proficiency.

5. A video based on how to Evaluate the Laplace Transform.

6. How to use this calculator?

Using the Laplace Transform Calculator is straightforward:

1. Input Function: Enter the time-domain function $f(t)$ or upload a table of multiple functions.
2. Click Calculate: Instantly view the Laplace Transform $F(s)$ for each input.
3. Analyze Results: Use the transformed functions for solving equations, analyzing systems, or other applications.

The tool handles standard and custom functions effortlessly, ensuring precise results every time.

7. Solved Examples on Laplace Transform

Example 1:

Find the Laplace Transform of $f(t) = \sin(2t)$

Solution:

1. Formula:

   $\mathcal{L}\{\sin(2t)\} = \dfrac{2}{s^2 + 4}$

2. Result:

   $F(s) = \dfrac{2}{s^2 + 4}$

Example 2: Tabular Data:

Steps:

1. Input the functions into the calculator.

2. Compute the Laplace Transform for each row.

8. Frequently Asked Questions (FAQs)

Q1. What is the Laplace Transform used for?

It’s used to convert time-domain functions into the frequency domain, simplifying the solution of differential equations and system analysis.

Q2. Can this calculator handle custom functions?

Yes, it supports both standard and custom time-domain functions.

Q3. Is this calculator free?

Yes, our Laplace Transform Calculator is completely free to use.

Q4. Does it support bulk data?

Absolutely, it’s designed to handle tabular data for bulk transformations.

Q5. Is it mobile-compatible?

Yes, the calculator works seamlessly on any device.

Q6. Can I export the results?

Yes, the outputs can be downloaded for further use or documentation.

Q7. Does it include standard Laplace Transform pairs?

Yes, the calculator provides a library of common transform pairs for quick reference.

Q8. Can I use it for inverse Laplace Transforms?

This version is specifically designed for forward Laplace Transforms, but an inverse version may be available separately.

9. What Are the Real-Life Applications?

The Laplace Transform Calculator is widely used in:

• Engineering: Analyze electrical circuits, mechanical systems, and control systems.
• Mathematics: Solve differential equations and integral equations.
• Physics: Model wave functions and dynamics.
• Data Science: Perform signal processing and system modeling.
• Education: Teach and learn advanced mathematical concepts.

Fictional Anecdote: Alex, an engineering student, used our Laplace Transform Calculator to solve a complex system of differential equations for a project. With accurate results and saved time, Alex confidently presented the findings and aced the project.

10. Conclusion

The Laplace Transform Calculator is an indispensable tool for simplifying complex mathematical operations. Its accuracy, speed, and user-friendly design make it ideal for students, educators, and professionals tackling advanced problems.

Ready to transform your mathematical challenges into solutions? Try our Laplace Transform Calculator today and experience the power of seamless calculations!

If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]

$\fcolorbox{black}{lightpink}{\color{blue}{Click here to Ask any Doubt}}$
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real time. Sign up and get registered with us.

$\color{red} \bold{Related \space Calculators}$
Hypergeometric Distribution Calculator
Normal Distribution Calculator
X and Y Intercepts Calculator
FOIL Method Calculator
Fraction to Percent Calculator
Logarithm Calculator
Cube Root Calculator