Matrices Addition or Subtraction Calculator

Get Homework Help

Neetesh Kumar | January 28, 2025 (Updated) $\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space$ Share this Page on:

Working with matrices can sometimes feel like juggling numbers in a puzzle. Whether you’re solving systems of equations, analyzing data, or studying linear algebra, the Matrices Addition or Subtraction Calculator simplifies the process. It’s a powerful tool that handles calculations for individual or tabular datasets, ensuring accuracy and efficiency.

1. Introduction to the Addition/Subtraction of two Matrices.

Welcome to the world of matrix operations, where mathematical prowess meets real-world applications. This blog will delve into the fascinating realms of matrix addition and subtraction. Whether you're a student grappling with linear algebra or a professional seeking to enhance your mathematical toolkit, understanding these operations is crucial. Let's embark on a journey that demystifies the essence of matrix addition and subtraction.
$\bold{Definition:}$ Matrices are mathematical entities that consist of rows and columns of numbers. Matrix addition involves combining two matrices to create a new matrix, while subtraction takes one matrix away from another. Both operations require matrices to have the same dimensions.

2. What is the formula used?

For matrix addition (A + B), the corresponding elements of matrices A and B are added together to follow the rule. $(A + B)_{ij}$ = $(A)_{ij}$ + $(B)_{ij}$

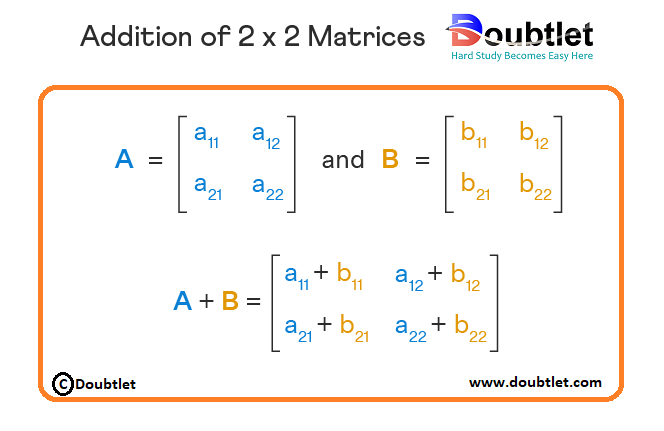
For matrix subtraction (A - B), the corresponding elements of matrices A and B are added together to follow the rule. $(A - B)_{ij}$ = $(A)_{ij}$ - $(B)_{ij}$

3. How do I add/subtract two Matrices?

To manually add or subtract matrices:

1. Ensure Equal Dimensions: Verify that both matrices have the same number of rows and columns.

2. Perform Element-Wise Operations: Add or subtract corresponding elements from each matrix.

3. Write the Resultant Matrix: Record the computed values in a new matrix.

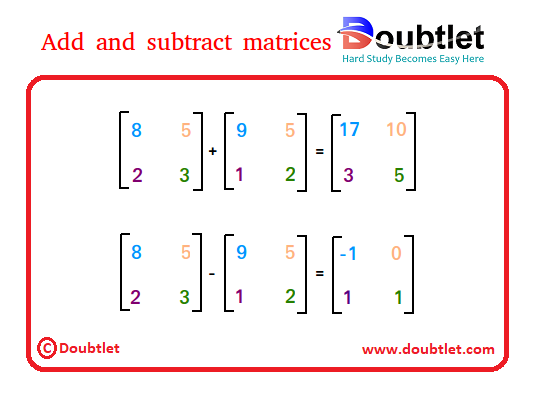
Example (Addition):

Matrix $A$ and $B$:

$A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}$

$C = A + B = \begin{bmatrix} 1+5 & 2+6 \\ 3+7 & 4+8 \end{bmatrix} = \begin{bmatrix} 6 & 8 \\ 10 & 12 \end{bmatrix}$

Example (Subtraction):

Matrix $A$ and $B$:

$A = \begin{bmatrix} 9 & 7 \\ 5 & 3 \end{bmatrix}, \quad B = \begin{bmatrix} 4 & 2 \\ 1 & 6 \end{bmatrix}$

$C = A - B = \begin{bmatrix} 9-4 & 7-2 \\ 5-1 & 3-6 \end{bmatrix} = \begin{bmatrix} 5 & 5 \\ 4 & -3 \end{bmatrix}$

Manual calculations become cumbersome with larger matrices, but our calculator streamlines the process for any matrix size.

4. Why choose our Matrices Addition/Subtraction Calculator?

$\bold{Easy \space \space to \space Use}$
Our calculator page provides a user-friendly interface that makes it accessible to both students and professionals. You can quickly input your square matrix and obtain the matrix of minors within a fraction of a second.

$\bold{Time \space Saving \space By \space automation}$
Our calculator saves you valuable time and effort. You no longer need to manually calculate each cofactor, making complex matrix operations more efficient.

$\bold{Accuracy \space and \space Precision}$
Our calculator ensures accurate results by performing calculations based on established mathematical formulas and algorithms. It eliminates the possibility of human error associated with manual calculations.

$\bold{Versatility}$
Our calculator can handle all input values like integers, fractions, or any real number.

$\bold{Complementary \space Resources}$
Alongside this calculator, our website offers additional calculators related to Pre-algebra, Algebra, Precalculus, Calculus, Coordinate geometry, Linear algebra, Chemistry, Physics, and various algebraic operations. These calculators can further enhance your understanding and proficiency.

5. A video based on the concept of Addition/Subtraction of two Matrices

6. How to use this calculator?

Using the Matrices Addition/Subtraction Calculator is simple:

1. Input the Matrices: Enter the elements of the two matrices or upload a table with multiple matrix pairs.
2. Select Operation: Choose between addition or subtraction.
3. Click Calculate: Instantly view the resulting matrix for each pair.
4. Analyze Results: Use the outputs for academic, professional, or personal purposes.

This tool saves time and ensures accurate results for all matrix operations.

7. Solved Examples on Addition/Subtraction.

$\bold{Question:1}$
Let's Add the given matrices as A + B where A = $\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ and B = $\begin{bmatrix} 2 & 2 \\ 3 & 5 \end{bmatrix}$
$\bold{Solution}$
The value of matrix A + B = $\begin{bmatrix} (1 + 2) & (2 + 2) \\ (3 + 3) & (4 + 5) \end{bmatrix}$. = $\begin{bmatrix} 3 & 4 \\ 6 & 9 \end{bmatrix}$

$\bold{Question:2}$
Let's subtract the given matrices as A - B where A = $\begin{bmatrix} 1 & 2 \\ -3 & 4 \end{bmatrix}$ and B = $\begin{bmatrix} -2 & 0.1 \\ 3 & \frac 2 3 \end{bmatrix}$
$\bold{Solution}$
The value of matrix A - B = $\begin{bmatrix} (1) - (-2) & (2) - (0.1) \\ (-3) - (3) & (4) - (\frac{2}{3}) \end{bmatrix}$. = $\begin{bmatrix} 3 & 1.9 \\ -6 & \frac {10} {3} \end{bmatrix}$

8. Frequently Asked Questions (FAQs)

Q1. Can matrices with different dimensions be added or subtracted?

No, matrix addition and subtraction require matrices to have the same dimensions. These operations are not defined if matrices have different numbers of rows or columns.

Q2. Is the order of matrices important in addition and subtraction?

Yes, the order of matrices is crucial in these operations. Matrices must be the same size for addition and subtraction to be valid. The corresponding elements of the matrices are added or subtracted based on their positions.

Q3. Can I add or subtract more than two matrices together?

Certainly! Matrix addition and subtraction are associative operations, meaning you can add or subtract multiple matrices together. Ensure that all matrices involved have the same dimensions.

Q4. What happens if I add or subtract matrices with different data types?

Using matrices with consistent data types in standard matrix operations is essential. Mixing data types may lead to unexpected results or errors. Ensure all elements within matrices are the same type (e.g., integers or decimals).

Q5. Are there any shortcuts or rules for matrix addition and subtraction?

Matrix addition and subtraction follow straightforward rules, adding or subtracting corresponding elements. No specific shortcuts exist, but you can simplify the process by ensuring matrices have the same dimensions before performing these operations. Additionally, reviewing the order of matrices and their sizes is fundamental to a successful computation.

9. What Are the Real-Life Applications?

Matrix addition and subtraction are widely used in:

• Computer Graphics: Combine transformations for rendering images.
• Data Science: Manipulate datasets represented as matrices.
• Engineering: Solve systems of linear equations.
• Economics: Model resource allocation problems.
• Education: Teach and learn linear algebra concepts.

Fictional Anecdote: Priya, a computer science student, uses our calculator to combine transformation matrices for a graphics project. With accurate results, she confidently implements animations for her assignment.

10. Conclusion

Mastering matrix addition and subtraction opens the door to many applications in mathematics and beyond. Whether exploring linear algebra's intricacies or applying these operations in real-world scenarios, a solid understanding of these fundamental concepts is indispensable. As you navigate the world of matrices, may your mathematical journey be enlightening and empowering.

If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]

$\fcolorbox{black}{lightpink}{\color{blue}{Click here to Ask any Doubt}}$
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real time. Sign up and get registered with us.

$\color{red} \bold{Related \space Calculators}$
$\bold{Matrix \space Multiplication}$
$\bold{Matrix \space Division}$
$\bold{Trace \space of \space a \space Matrix}$
$\bold{Transpose \space of \space a \space Matrix}$
$\bold{Matrix \space of \space Minors}$
$\bold{Matrix \space of \space Cofactors}$
$\bold{Determinant \space of \space a \space Matrix}$