Matrix of Cofactors Calculator

$\color{red} \bold{Related \space Calculators:}$
Inverse of a matrix
Adjoint of a Matrix
Matrix multiplication
Rank of a Matrix
Cramer's Rule
Row echelon form of a matrix

$\bold{Table \space of \space Content}$

• 1. Introduction to the matrix of cofactors
• 2. What are the conditions required?
• 3. How do I calculate the cofactor matrix?
• 4. Why choose our Matrix of Cofactor Calculator?
• 5. A Video for explaining this concept
• 6. How to use this calculator?
• 7. Solved Examples
• 8. Frequently Asked Questions (FAQs)
• 9. What are the Real-life applications?
• 10. Conclusion

1. Introduction to the Matrix of Cofactors

Matrices are a fundamental concept in linear algebra, and understanding their properties and operations is crucial in various fields of science and engineering. One important matrix associated with another matrix is the matrix of cofactors. In this blog, we will explore the matrix of cofactors, the conditions required for its existence, and the formula used to compute it. We will also provide step-by-step instructions along with solved examples to make the concept clear. Additionally, we'll discuss real-life applications and answer frequently asked questions to help you grasp the practical significance of this mathematical concept.
$\bold{Definition}$
The matrix of cofactors, often denoted as C, is a square matrix derived from another square matrix, typically called matrix A. Each element of the matrix of cofactors corresponds to the cofactor of the corresponding component of matrix A. A cofactor is obtained by removing the matrix's determinant and removing the row and column containing that element.

2. What are the conditions required?

$\bold{Square \space Matrix}$
Matrix of Cofactors is only defined for square matrices, which means matrices with an equal number of rows and columns. You cannot calculate its cofactor matrix if you have an m x n matrix where m ≠ n.

$\bold{Non \space singularity}$
A matrix must be non-singular (or invertible) to have a determinant. In other words, its determinant must not be equal to zero. A zero determinant indicates that the matrix does not have a unique inverse.

$\bold{Order \space of \space the \space Matrix}$
The order of a matrix determines the number of elements involved in the determinant calculation. For an n x n matrix, the matrix involves $n^2$ terms.

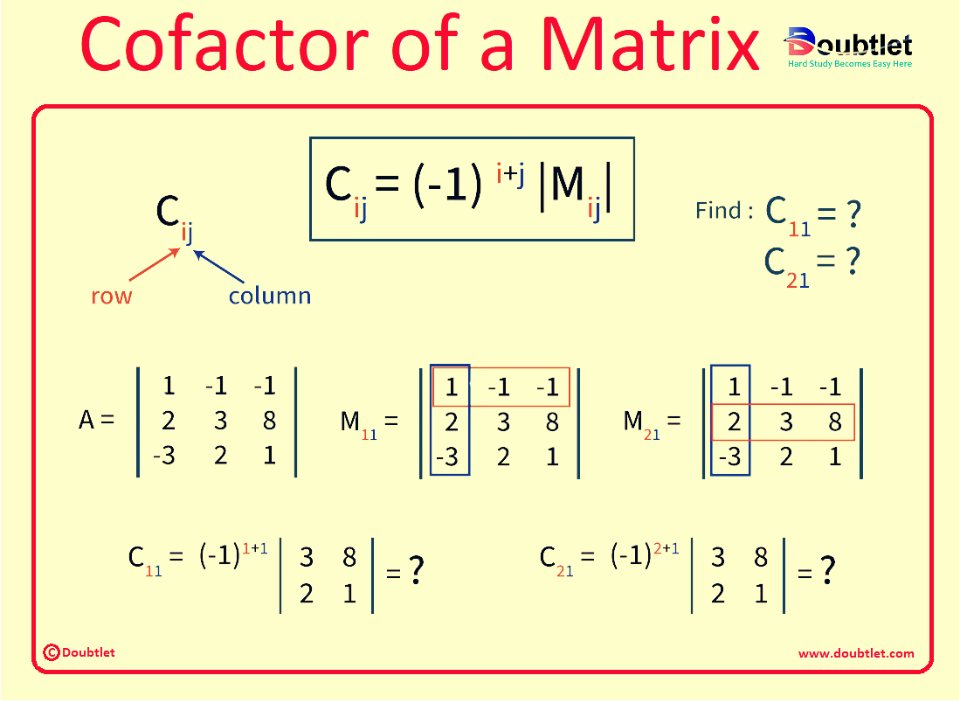
3. How do I calculate the Matrix of Cofactors of a given matrix?

Verify whether the matrix is a Square matrix or not.
Identify the order of the matrix.
Obtain the Minor of every element.
The formula to find the matrix of cofactors C for a square matrix A is as follows:
$C_{ij}$ = $(-1)^{i + j}.det(M_{ij})$ ,
where
$C_{ij}$ is the cofactor at the $i^{th}$ row and $j^{th}$ column of matric C.
$M_{ij}$ is the matrix obtained by removing the $i^{th}$ row and $j^{th}$ column from the matrix A.
$det(M_{ij})$ is the determinant of matrix $M_{ij}$
That's the step-by-step process of calculating the matrix of cofactors using the expansion by minors method.

4. Why choose our Matrix of Cofactors Calculator?

$\bold{Easy \space \space to \space Use}$
Our calculator page provides a user-friendly interface that makes it accessible to both students and professionals. You can quickly input your square matrix and obtain the matrix of minors within a fraction of a second.

$\bold{Time \space Saving \space By \space automation}$
Our calculator saves you valuable time and effort. You no longer need to manually calculate each cofactor, making complex matrix operations more efficient.

$\bold{Accuracy \space and \space Precision}$
Our calculator ensures accurate results by performing calculations based on established mathematical formulas and algorithms. It eliminates the possibility of human error associated with manual calculations.

$\bold{Versatility}$
Our calculator can handle all input values like integers, fractions, or any real number.

$\bold{Complementary \space Resources}$
Alongside this calculator, our website offers additional calculators related to Pre-algebra, Algebra, Precalculus, Calculus, Coordinate geometry, Linear algebra, Chemistry, Physics, and various algebraic operations. These calculators can further enhance your understanding and proficiency.

5. A detailed video based on the concept of the Matrix of Cofactors.

6. How to use this calculator

This calculator will help you to find the matrix of cofactors of a square matrix of any order.
You have to put all the matrix elements in the given input boxes.
A step-by-step solution will be displayed on the screen after clicking the Calculate button.
You can access, download, and share the solution.

7. Solved Examples

$\bold{Question:1}$
Let's calculate the matrix of cofactors for a 2x2 matrix $\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$.
$\bold{Solution:1}$
The matrix of cofactors of the above-given matrix is $\begin{bmatrix} 4 & -3 \\ -2 & 1 \end{bmatrix}$.

$\bold{Question:2}$
Let's calculate the matrix of cofactors for a 3x3 matrix $\begin{bmatrix} 1 & 2 & 3 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{bmatrix}$.
$\bold{Solution:2}$
The matrix of cofactors of the above-given matrix is $\begin{bmatrix} -3 & 6 & -3 \\ 6 & -12 & 6 \\ -3 & 6 & -3 \end{bmatrix}$.

8. Frequently Asked Questions (FAQs):-

1. What is the significance of the matrix of cofactors in linear algebra?

The matrix of cofactors is important for various applications in linear algebra, such as finding the inverse of a matrix, solving systems of linear equations, and calculating determinants.

2. Can the matrix of cofactors be used to find the adjugate of a matrix?

Yes, the matrix of cofactors is a key component in finding the adjugate of a matrix, which is essential for calculating the inverse of a matrix.

3. Are there any shortcuts or techniques to compute the matrix of cofactors faster?

While the formula for cofactors involves calculating determinants, methods like Cramer's rule can simplify the process of finding determinants and, consequently, the matrix of cofactors for small-sized matrices.

4. Can you find the matrix of cofactors for non-square matrices?

No, the matrix of cofactors is defined only for square matrices, where the number of rows equals the number of columns.

5. What are the signs of cofactors, and how are they determined?

The sign of each cofactor depends on the element's position in the matrix. Cofactors for elements in odd-numbered rows and columns have positive signs, while those in even-numbered rows and columns have negative signs.

9. What are the Real-life applications?

Understanding the matrix of cofactors is not just a theoretical exercise; it has practical applications in various fields, including:
$\bold{Engineering:}$ Engineers use a matrix of cofactors techniques to solve complex systems of linear equations in structural analysis and electrical circuit analysis.
$\bold{Statistics:}$ matrices play a crucial role in data analysis, and the matrix of cofactors can be used in multivariate statistical analysis.
$\bold{Computer \space Graphics:}$ Transformations and projections in computer graphics often involve matrices, and the matrix of cofactors can be useful for various graphical transformations.

10. Conclusion

The matrix of cofactors is a valuable concept in linear algebra, serving as a building block for various mathematical operations and practical applications. By understanding its definition, conditions, formula, and how to compute it step by step, you gain a deeper insight into the world of matrices and their role in solving real-world problems. Whether you are an engineer, scientist, or a mathematics student, mastering the matrix of cofactors is a significant step toward enhancing your problem-solving skills in various domains.

This blog is written by Neetesh Kumar

If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]

$\fcolorbox{black}{lightpink}{\color{blue}{Click here to Ask any Doubt}}$
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real-time. Sign up and get registered with us.