Percentile Rank Calculator

Get Homework Help

Neetesh Kumar | January 05, 2025 $\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space$ Share this Page on:

Understanding your position in a dataset, whether it's test scores, sales data, or survey results, often boils down to one concept: percentile rank. The Percentile Rank Calculator for a Table is an essential tool for professionals, students, and analysts alike. Let's unpack its utility, formulas, and how it can help you gain sharper insights into your data.

1. Introduction to the Percentile Rank Calculator

The Percentile Rank Calculator determines how a particular value compares to the rest of the dataset. In simpler terms, it tells you the percentage of data points that fall below a specific value. For example, if your test score is in the 90th percentile, you've performed better than $90$ of participants.

This calculator works seamlessly with tabular data, handling rows and columns effortlessly to provide accurate results with minimal effort.

2. What is the Formulae used?

The formula for percentile rank is:

$P = \dfrac{\text{Number of Values Below } X + 0.5}{\text{Total Number of Values}} \times 100$

Where:

• $P$: Percentile rank
• $X$: The value whose percentile rank is being calculated.

For example: If a dataset has $20$ values and $18$ are below $X$:

$P = \dfrac{18 + 0.5}{20} \times 100 = 92.5\%$

This method ensures precision, even for tied values.

3. How do I find the Percentile Rank?

Calculating the percentile rank manually involves:

1. Sorting the data: Arrange values in ascending order.
2. Counting values below $X$: Identify how many entries are less than the target value.
3. Applying the formula: Use the formula to calculate the rank.

Example: Dataset: $[40, 50, 60, 70, 80, 90]$

Find the percentile rank of $X = 70$:

• Values below $X = 3$
• Total values = 6

$P = \dfrac{3 + 0.5}{6} \times 100 = 58.3\%$

For large datasets, let’s face it manual calculations are tedious. That’s where our calculator steps in, making your life easier.

4. Why Choose Our Percentile Rank Calculator for a Table?

$\bold{Easy \space \space to \space Use}$
Our calculator page provides a user-friendly interface that makes it accessible to both students and professionals. You can quickly input your square matrix and obtain the matrix of minors within a fraction of a second.

$\bold{Time \space Saving \space By \space automation}$
Our calculator saves you valuable time and effort. You no longer need to manually calculate each cofactor, making complex matrix operations more efficient.

$\bold{Accuracy \space and \space Precision}$
Our calculator ensures accurate results by performing calculations based on established mathematical formulas and algorithms. It eliminates the possibility of human error associated with manual calculations.

$\bold{Versatility}$
Our calculator can handle all input values like integers, fractions, or any real number.

$\bold{Complementary \space Resources}$
Alongside this calculator, our website offers additional calculators related to Pre-algebra, Algebra, Precalculus, Calculus, Coordinate geometry, Linear algebra, Chemistry, Physics, and various algebraic operations. These calculators can further enhance your understanding and proficiency.

5. A video based on how to Evaluate the Percentile Rank.

6. How to use this calculator?

Using our Percentile Rank Calculator is as easy as:

1. Input your data: Enter or paste values from your table.
2. Specify the target value $X$: Provide the value whose percentile rank you want to find.
3. Click calculate: The percentile rank is displayed instantly.

You don’t need to be a math wizard to get accurate results. Just a few clicks and you’re good to go.

7. Solved Examples on Percentile Rank

Example 1:

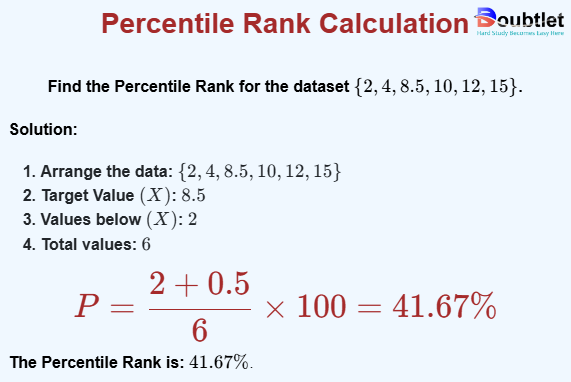
Find the Percentile Rank for the dataset $\{5, 10, 15, 20, 25, 30\}$.

Solution:

1. Arrange the data: $\{5, 10, 15, 20, 25, 30\}$
2. Target Value $(X)$: $20$
3. Values below $(X)$: $3$
4. Total values: $6$

$P = \dfrac{3 + 0.5}{6} \times 100 = 58.3\%$

The Percentile Rank is: $58.3\%$.

Example 2: Tabular Data:

Solution:

Find percentile rank for $X = 75$:

• Values below $75$: $1$
• Total values: $4$

$P = \dfrac{1 + 0.5}{4} \times 100 = 37.5\%$

The Percentile Rank is: $37.5\%$.

Our calculator handles these calculations with lightning speed.

8. Frequently Asked Questions (FAQs)

Q1. What is percentile rank in statistics?

It indicates the percentage of data points below a particular value in a dataset.

Q2. Does the calculator support large datasets?

Yes, it handles thousands of entries efficiently.

Q3. Can I calculate ranks for multiple values simultaneously?

Absolutely! Just input the values as a table.

Q4. Does it adjust for tied values?

Yes, the calculator accounts for ties with precision.

Q5. Is this tool free?

Yes, it’s $100$ free to use.

Q6. Can I use it for ranked data?

Yes, you can calculate percentile ranks for pre-ranked data too.

Q7. Is the calculator mobile-friendly?

Yes, it works seamlessly across all devices.

Q8. What types of data can I input?

The calculator supports numerical and ordinal data.

9. What are the real-life applications?

Percentile rank calculations are invaluable in many fields:

• Education: Evaluate student performance compared to peers.
• Business Analytics: Understand sales performance relative to competitors.
• Healthcare: Analyze patient data to determine population trends.
• Sports: Rank players based on performance metrics.
• Market Research: Identify consumer preferences within a demographic.

Fictional anecdote: Imagine Maria, a market analyst. She uses the Percentile Rank Calculator to rank products based on sales performance. By identifying the top $10$ of products, Maria creates a targeted marketing strategy that doubles her company’s revenue. Talk about working smarter, not harder!

10. Conclusion

The Percentile Rank Calculator is more than just a tool it’s a must-have for anyone dealing with data. With its simplicity, speed, and accuracy, it transforms a potentially time-consuming process into a matter of seconds. Whether you’re analyzing test scores, business metrics, or survey data, this calculator ensures you’re always on point.

Try it today and experience the difference. Because in the world of numbers, knowing your rank can make all the difference.

If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]

$\fcolorbox{black}{lightpink}{\color{blue}{Click here to Ask any Doubt}}$
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real time. Sign up and get registered with us.

$\color{red} \bold{Related \space Calculators}$
Range of Data Set Calculator
Linear Regression (Line of best fit) Calculator
Euler's Method calculator
Quadratic Regression (Parabola of best fit) Calculator
Root Mean Square (RMS) Value Calculator
Covariance Calculator
Standard Deviation Calculator