Poisson Distribution Calculator

Get Homework Help

Neetesh Kumar | January 09, 2025 $\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space$ Share this Page on:

The Poisson Distribution is a cornerstone of probability theory, widely used for modeling events that occur at a constant rate over a specific interval. The Poisson Distribution Calculator for a Table takes the guesswork out of these calculations, providing accurate results quickly and easily. Whether you’re a student, researcher, or data analyst, this tool is designed to streamline your computations.

1. Introduction to the Poisson Distribution Calculator

The Poisson Distribution describes the probability of a certain number of events happening within a fixed interval, given a known average rate ($\lambda$). It’s commonly used to model rare events, such as customer arrivals, system failures, or natural phenomena.

Our Poisson Distribution Calculator makes it easy to analyze data in tabular form, helping you calculate probabilities, cumulative values, and more. From predicting call center traffic to analyzing machine breakdowns, this calculator is an indispensable tool.

2. What is the Formulae used?

The formula for the Poisson Distribution is:

$P(X = k) = \dfrac{\lambda^k e^{-\lambda}}{k!}$

Where:

• $P(X = k)$: Probability of $k$ events occurring.
• $\lambda$: Average number of events in the interval.
• $k$: Number of events ($0, 1, 2, \dots$).
• $e$: Euler’s number, approximately $2.718$.

Cumulative Distribution Function (CDF):

The CDF is the probability of $X$ being less than or equal to $k$:

$P(X \leq k) = \displaystyle\sum_{i=0}^{k} \dfrac{\lambda^i e^{-\lambda}}{i!}$

These formulas allow you to calculate both individual probabilities and cumulative probabilities, giving a complete view of the distribution.

3. How Do I Find the Poisson Distribution?

To calculate the Poisson Distribution manually:

1. Identify Parameters: Determine $\lambda$ (average rate) and $k$ (number of events).
2. Use the Formula: Substitute $\lambda$ and $k$ into the formula.
3. Compute Factorial: Calculate $k!$, the factorial of $k$.
4. Evaluate: Solve for $P(X = k)$.

Example:
If $\lambda = 4$ and $k = 3$:

$P(X = 3) = \dfrac{4^3 e^{-4}}{3!} = \dfrac{64 \times 0.0183}{6} \approx 0.195$

For cumulative probabilities or larger datasets, manual calculations can be cumbersome. That’s where our calculator comes in handy.

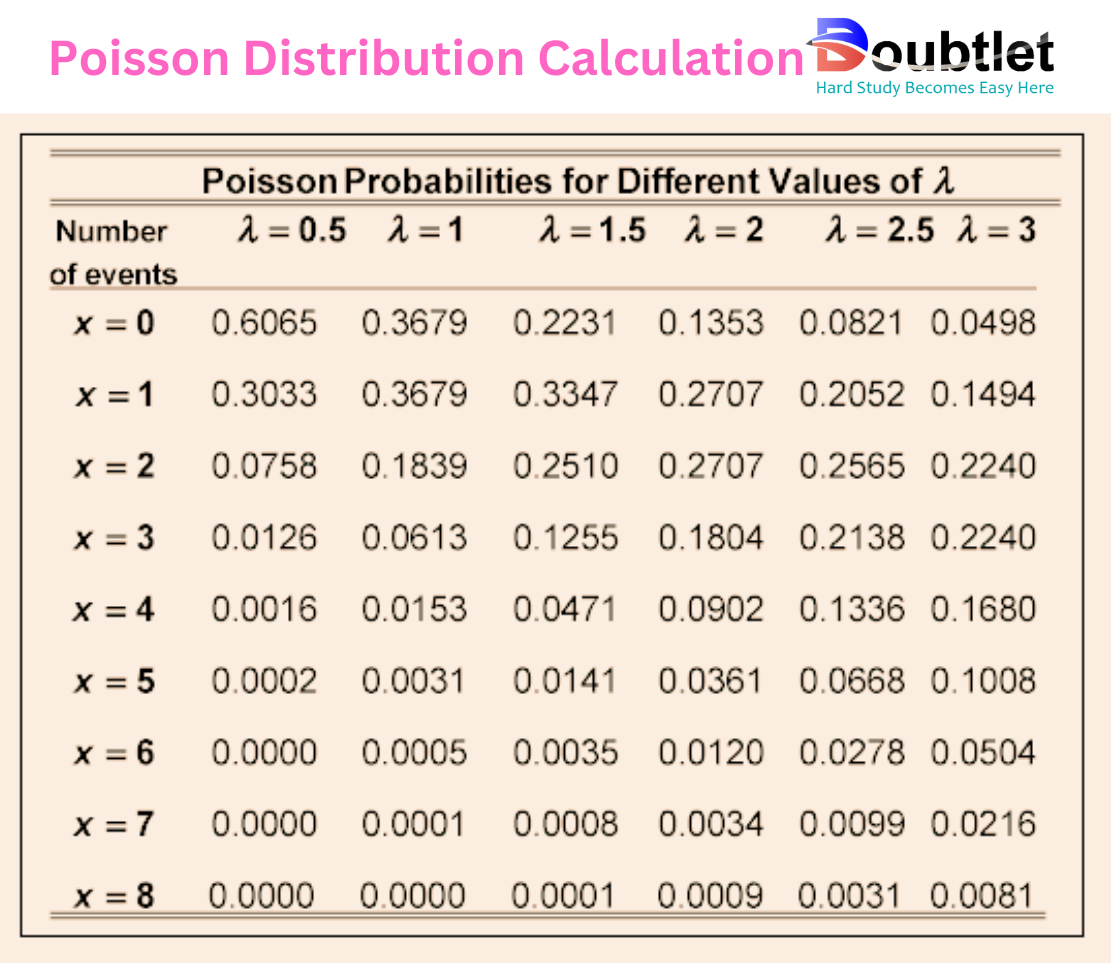
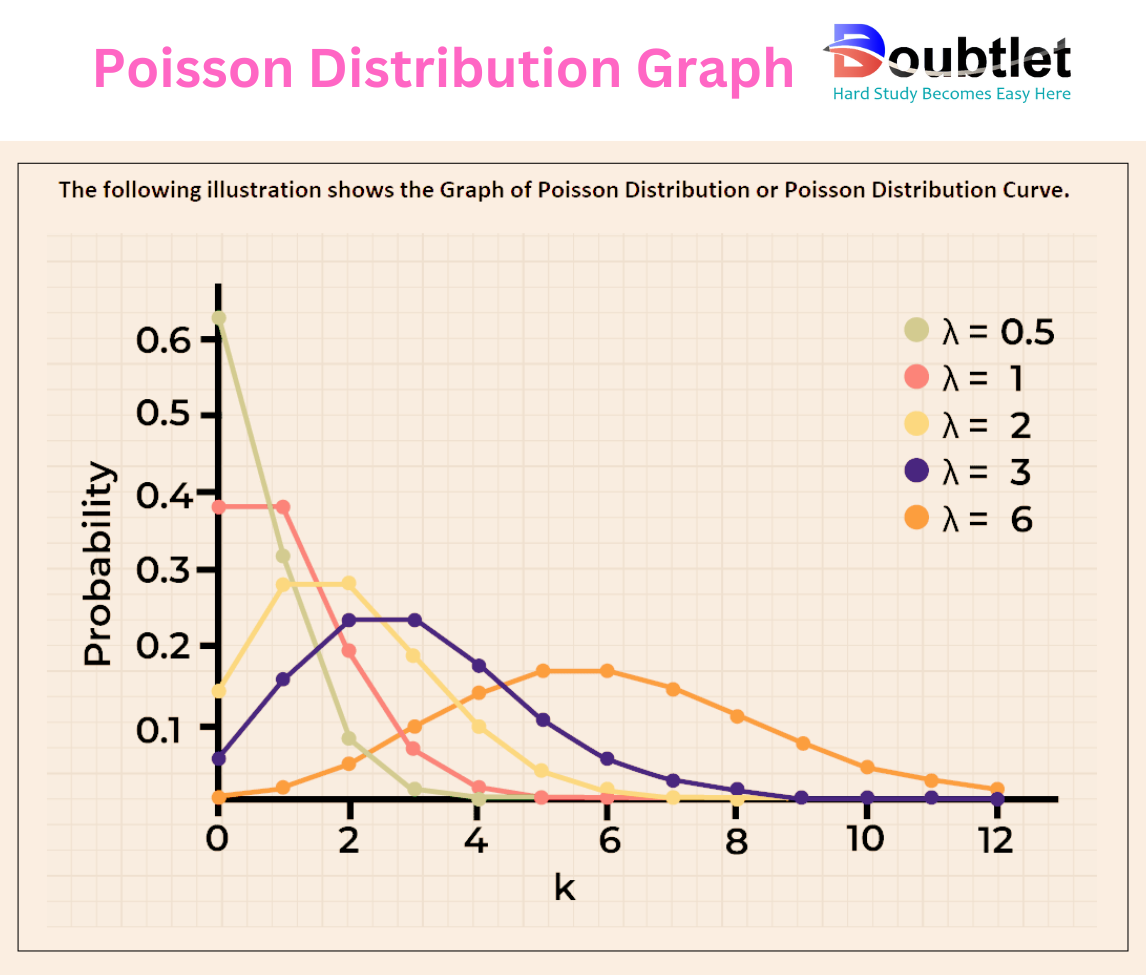
4. Why Choose Our Poisson Distribution Calculator?

$\bold{Easy \space \space to \space Use}$
Our calculator page provides a user-friendly interface that makes it accessible to both students and professionals. You can quickly input your square matrix and obtain the matrix of minors within a fraction of a second.

$\bold{Time \space Saving \space By \space automation}$
Our calculator saves you valuable time and effort. You no longer need to manually calculate each cofactor, making complex matrix operations more efficient.

$\bold{Accuracy \space and \space Precision}$
Our calculator ensures accurate results by performing calculations based on established mathematical formulas and algorithms. It eliminates the possibility of human error associated with manual calculations.

$\bold{Versatility}$
Our calculator can handle all input values like integers, fractions, or any real number.

$\bold{Complementary \space Resources}$
Alongside this calculator, our website offers additional calculators related to Pre-algebra, Algebra, Precalculus, Calculus, Coordinate geometry, Linear algebra, Chemistry, Physics, and various algebraic operations. These calculators can further enhance your understanding and proficiency.

5. A video based on how to Evaluate the Poisson Distribution.

6. How to use this calculator?

Using the Poisson Distribution Calculator is straightforward:

1. Enter Parameters: Input the average rate ($\lambda$) and the number of events ($k$).
2. Choose Output: Select individual probabilities or cumulative probabilities.
3. Click Calculate: Instantly view the results, including detailed steps.

Our tool simplifies the process, letting you focus on interpreting the results.

7. Solved Examples on Poisson Distribution

Example 1: Defects in Manufacturing:

Scenario: A factory produces an average of $0.5$ defective items per hour. What is the probability that there will be $2$ defective items in an hour?

Solution: Here, $\lambda = 0.5$ and $k = 2$.

Using the Poisson formula:

$P(2; 0.5) = \dfrac{0.5^2 e^{-0.5}}{2!}$

Simplify:

$P(2; 0.5) = \dfrac{0.25 \cdot e^{-0.5}}{2} \approx 0.0758$

Result: The probability of $2$ defective items in an hour is approximately $0.0758$ or $7.58\%$.

Example 2: Website Visits:

Scenario: A website experiences an average of $3$ visits per minute. What is the probability of getting $5$ visits in a minute?

Solution: Here, $\lambda = 3$ and $k = 5$.

Using the Poisson formula:

$P(5; 3) = \dfrac{3^5 e^{-3}}{5!}$

Simplify:

$P(5; 3) = \dfrac{243 \cdot e^{-3}}{120} \approx 0.1008$

Result: The probability of receiving $5$ visits in a minute is approximately $0.1008$ or $10.08\%$.

Example 3: Tabular Data:

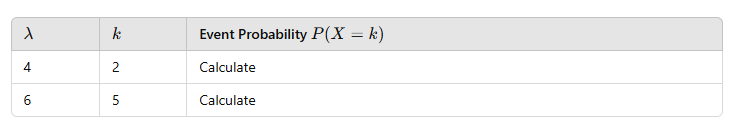
Steps:

1. Input each row into the calculator.
2. Compute probabilities for each pair of $\lambda$ and $k$.

Our calculator provides these results instantly and accurately.

8. Frequently Asked Questions (FAQs)

Q1. What is the Poisson Distribution used for?

It models the probability of a given number of events occurring in a fixed interval, given a constant average rate.

Q2. What is $\lambda$ in the Poisson Distribution?

$\lambda$ represents the average rate of occurrences.

Q3. Is this calculator free to use?

Yes, our Poisson Distribution Calculator is completely free.

Q4. Can it handle large datasets?

Yes, it supports extensive tabular data.

Q5. Does it calculate cumulative probabilities?

Yes, it computes both individual and cumulative probabilities.

Q6. Is the calculator mobile-friendly?

Absolutely, it works seamlessly on all devices.

Q7. Can I export results?

Yes, you can download results for further analysis.

Q8. Does the calculator show intermediate steps?

Yes, it provides detailed calculations for better understanding.

9. What are the real-life applications?

The Poisson Distribution is widely used in:

• Customer Service: Predict call volumes or service requests.
• Healthcare: Model the arrival of patients in emergency rooms.
• Manufacturing: Analyze machine failures or defects.
• Traffic Management: Predict the arrival rate of vehicles at toll booths.
• Natural Events: Model rare events like earthquakes or lightning strikes.

Fictional anecdote: Jane, a logistics manager, uses the Poisson Distribution Calculator to estimate package arrival rates at a sorting center. With accurate predictions, she optimizes staffing levels, reducing costs and improving efficiency.

10. Conclusion

The Poisson Distribution Calculator is an essential tool for analyzing probabilities in events with a fixed average rate. By automating complex calculations, it saves time, ensures accuracy, and provides valuable insights for professionals and students alike.

Ready to analyze your data with ease? Try our Poisson Distribution Calculator today and uncover the power of probability!

If you have any suggestions regarding the improvement of the content of this page, please write to me at My Official Email Address: [email protected]

$\fcolorbox{black}{lightpink}{\color{blue}{Click here to Ask any Doubt}}$
Are you Stuck on homework, assignments, projects, quizzes, labs, midterms, or exams?
To get connected to our tutors in real time. Sign up and get registered with us.

$\color{red} \bold{Related \space Calculators}$
Coefficient of Variation Calculator
Beta Distribution Calculator
P Value Calculator
Box and Whisker Plot Calculator
Z Score Calculator
Binomial Distribution Calculator
Exponential Distribution Calculator