3d-coordinate-geometry Formula Sheet

In three-dimensional space, a line is a straight path that extends infinitely in two opposite directions, defined by a point and a direction vector. Conversely, a plane is a flat surface extending infinitely in all directions, defined by a point and two non-parallel direction vectors or by a point and a normal vector perpendicular to the plane.

Neetesh Kumar | May 08, 2024 $\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space$ Share this Page on:

• 1. Distance Formula in 3-D
• 2. Section Formula in 3-D
• 3. Centroid of a Triangle in 3-D
• 4. Direction Cosines of a Line
• 5. Direction Ratios of a Line
• 6. Relation between Direction cosines & Direction Ratios
• 7. Direction Ratios & Cosines of a Line joining two Points
• 8. Projection of a Line on another line
• 9. Angle between two lines in 3-D
• 10. Condition for Parallel and Perpendicular Lines in 3-D
• 11. Equation of Lines in Parametric form
• 12. Length & Equation of Perpendicular from a point to a Line
• 13. Equation of Planes in various forms
• 14. The angle between two Planes
• 15. The angle between a line and Plane
• 16. Condition for Line to lie on Plane
• 17. Position of two points with respect to a Plane
• 18. Image of a Point in the Plane
• 19. Condition for the Lines to be Coplanar
• 20. Distance of a Point from the Plane
• 21. Equation of a Plane through the line of intersection of two planes
• 21. Angle Bisectors between two planes

1. Distance Formula in 3-D :

The distance between two points A ($x_1, y_1, z_1$) and B ($x_2, y_2, z_2$) in 3-d is given by AB = $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$

2. Section Formula in 3-D:

Let the point C (x, y, z) divide the line segment AB joining points A ($x_1, y_1, z_1$) and B ($x_2, y_2, z_2$) in the ratio of $m_1: m_2$, then Coordinates of Point C can be obtained as:
(x, y, z) = $\bigg(\frac{m_1x_2+m_2x_1}{m_1+m_2}, \frac{m_1y_2+m_2y_1}{m_1+m_2}, \frac{m_1z_2+m_2z_1}{m_1+m_2}\bigg)$

• If $\frac{m_1}{m_2}$ is $\bold{Positive}$, it means C divides the line segment AB $\bold{Internally}$.
  
• If $\frac{m_1}{m_2}$ is $\bold{Negative}$, it means C divides the line segment AB $\bold{Externally}$.
• Mid Point of AB is given by $\bigg(\frac{x_2+x_1}{2}, \frac{y_2+y_1}{2}, \frac{z_2+z_1}{2}\bigg)$

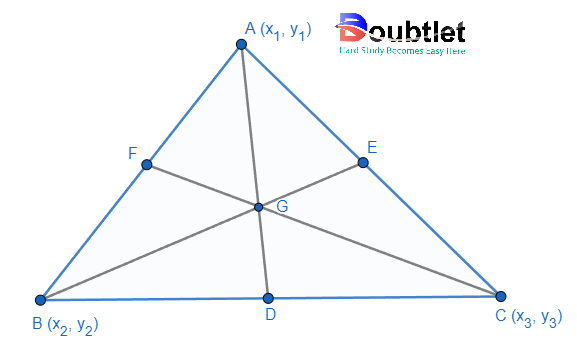
3. Centroid of a Triangle in 3-D:

Consider the points A ($x_1, y_1, z_1$), B ($x_2, y_2, z_2$) and C ($x_3, y_3, z_3$) be the vertices of a triangle ABC. Then its centroid G is given by
G = $(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3})$

4. Direction Cosines of a Line:

5. Direction Ratios of a Line:

Three numbers a, b, and c proportional to direction cosines l, m, n are called direction ratios of the line.
i.e. $\frac{l}{a} = \frac{m}{b} = \frac{n}{c}$ There exist infinitely many sets of direction ratios for a given line.

6. Relation between Direction cosines & Direction Ratios:

We know that $\frac{l}{a} = \frac{m}{b} = \frac{n}{c}$
Now, by squaring and adding the above terms
$\therefore \frac{l^2}{a^2} = \frac{m^2}{b^2} = \frac{n^2}{c^2} = \frac{l^2+m^2+n^2}{a^2+b^2+c^2}$
$\therefore$ $l = \frac{\plusmn a}{\sqrt{a^2+b^2+c^2}};$ $m = \frac{\plusmn b}{\sqrt{a^2+b^2+c^2}};$ $n = \frac{\plusmn c}{\sqrt{a^2+b^2+c^2}}$

7. Direction Ratios & Cosines of a Line joining two Points:

Let P ($x_1, y_1, z_1$) and Q ($x_2, y_2, z_2$) be two points of a line segment, then Direction Ratios of PQ are $(x_2 - x_1, y_2 - y_1, z_2 - z_1)$ and Direction Cosines are $\frac{x_2 - x_1}{r},$ $\frac{y_2 - y_1}{r},$ $\frac{z_2 - z_1}{r}$ where r = $|\overrightarrow{AB}|$ is the distance between A and B.

8. Projection of a Line on another line:

Let AB be a line segment with A ($x_1, y_1, z_1$) and B ($x_2, y_2, z_2$), and let L be a straight line whose direction cosines are l, m, n. Then the length of the projection of AB on the line L is $|l(x_2 - x_1) + m(y_2 - y_1) + n(z_2 - z_1)|$

9. Angle between two lines in 3-D:

Consider two lines with direction cosines $l_1, m_1, n_1$ and $l_2, m_2, n_2$ and angle between them is $\theta$ then cos$\theta =l_1l_2 + m_1m_2 + n_1n_2.$
If the direction ratios of these lines are $a_1, b_1, c_1$ and $a_2, b_2, c_2$ then Cos$\theta = \frac{a_1a_2 + b_1b_2 + c_1c_2}{\sqrt{(a_1^2+b_1^2+c_1^2)}\sqrt{(a_2^2+b_2^2+c_2^2)}}$

10. Condition for Parallel and Perpendicular Lines in 3-D:

$\bold{(a)}$ Consider two lines with direction cosines $l_1, m_1, n_1$ and $l_2, m_2, n_2$.

• These lines are Perpendicular if $\theta=90^o$ i.r. cos$\theta=0$ i.e. $\bold{(l_1l_2+m_1m_2+n_1n_2=0)}$
• These lines are Parallel if $\theta=0^o$ i.e. sin$\theta=0$ i.e. $\bold{\frac{l_1}{l_2}=\frac{m_1}{m_2}=\frac{n_1}{n_2}}$

$\bold{(b)}$ Consider two lines with direction ratios $a_1, b_1, c_1$ and $a_2, b_2, c_2$.

• These lines are Perpendicular if $\theta=90^o$ i.r. cos$\theta=0$ i.e. $\bold{(a_1a_2+b_1b_2+c_1c_2=0)}$
• These lines are Parallel if $\theta=0^o$ i.e. sin$\theta=0$ i.e. $\bold{\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}}$

11. Equation of Lines in Parametric form:

$\bold{(a)}$ Let the Equation of the line through two points be a given point on the line and l, m, n the direction cosines of the line, then its equation is
$\frac{x-x_1}{l} = \frac{y-y_1}{m} = \frac{z-z_1}{n} = t$ (let)
From the above equation, the general point on the line is P $(x_1+tl, x_2+tm, x_3+tn)$ and it is located at a distance of t units from the point A $(x_1, y_1, z_1)$ i.e. AP = t. This condition only holds for direction cosines but not for direction ratios.
If a, b, and c are the direction ratios of the line, then the equation of the line is
$\frac{x-x_1}{a} = \frac{y-y_1}{b} = \frac{z-z_1}{c} = t$ (let)
but here AP $\ne$ r

$\bold{(b)}$ Equation of the line through two points A $(x_1, y_1, z_1)$ and B $(x_2, y_2, z_2)$ is $\frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} = \frac{z-z_1}{z_2-z_1}$

12. Length & Equation of Perpendicular from a point to a Line:

Let equation of the line be $\frac{x-x_1}{l} = \frac{y-y_1}{m} = \frac{z-z_1}{n} = r$ (let) ....(i)
and A ($\alpha, \beta, \gamma$) be the point.
Then any general point on the line (i) is P ($lr + x_1, mr + y_1, nr + z_1$) .....(ii)
If it is the foot of the perpendicular, from A on the line, then AP is $\perp$ to the line,
So $l(r + x_1 - \alpha) + m(mr + y_1 - \beta) + n(nr + z_1 - \gamma) = 0$ i.e.
r = $(\alpha - x_1)l + (\beta - y_1)m + (\gamma - z_1)n$
Since $l^2 + m^2 + n^2 = 1$
Putting this value of r in (ii), we get the foot of the perpendicular from point A to the line.

$\bold{Length:}$ Since the foot of perpendicular P is known, the length of perpendicular is
AP = $\sqrt{[(lr+x_1-\alpha)^2 + (mr+y_1-\beta)^2 + (nr+z_1-\gamma)^2]}$
Equation of Perpendicular: $\frac{x-\alpha}{lr+x_1-\alpha} = \frac{y-\beta}{mr+y_1-\beta} = \frac{z-\gamma}{nr+z_1-\gamma}$

13. Equation of Planes in various forms:

The equation of every plane is of the first degree, i.e., of the form ax + by + cz + d = 0, in which a, b, and c are constants, where $a^2+b^2+c^2\ne0$ (i.e., a, b, and c $\ne 0$ simultaneously).
$\bold{(a)}$ Vector form of equation of plane :
If $\vec{a}$ is the position vector of a point on the plane and $\vec{n}$ is a vector normal to the plane,
then its vectorial equation is given by
($\vec{r}$ - $\vec{a}$).$\vec{n} = 0 \Rightarrow \vec{r}.\vec{n}=d$ where $d = \vec{a}.\vec{n}=constant.$

$\bold{(b)}$ Planes Parallel to the Coordinate Planes :

• The equation of the y-z plane is x = 0.
• The equation of the z-x plane is y = 0.
• The equation of the x-y plane is z = 0.
• The equation of the plane parallel to the x-y plane at a distance c is z = c. Similarly, planes parallel to the y-z and z-x planes are x = c and y = c respectively.

$\bold{(c)}$ Equations of Planes Parallel to the Axes :

• If a = 0, the plane is parallel to the x-axis, i.e., the equation of the plane parallel to the x-axis is by + cz + d = 0.
• Similarly, equations of planes parallel to the y-axis and parallel to the z-axis are ax + cz + d = 0 and ax + by + d = 0, respectively.

$\bold{(d)}$ Equation of a Plane in Intercept Form :
The equation of the plane which cuts off intercepts a, b, and c from the axes is $\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$

$\bold{(e)}$ Equation of a Plane in Normal Form :
If the length of the perpendicular distance of the plane from the origin is p and the direction cosines of this perpendicular are (l, m, n), then the equation of the plane is lx + my + nz = p.

$\bold{(f)}$ Vectorial form of Normal equation of plane :
If $\hat{n}$ is a unit vector normal to the plane from the origin to the plane and d be the perpendicular distance of the plane from the origin, then its vector equation is $\vec{r}.\hat{n}=d$

$\bold{(g)}$ Equation of a Plane through three points :
The equation of the plane through three non-collinear points A($x_1, y_1, z_1$), B($x_2, y_2, z_2$), C($x_3, y_3, z_3$) is $\begin{vmatrix} x & y & z & 1 \\ x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ x_3 & y_3 & z_3 & 1 \\ \end{vmatrix} = 0$

14. The angle between two Planes:

• Consider two planes ax + by + cz + d = 0 and a' x + b' y + c' z + d' = 0.
  The angle between these planes is the angle between their normals.
  Cos$\theta = \frac{aa' + bb' + cc'}{\sqrt{a^2+b^2+c^2}\sqrt{a'^2+b'^2+c'^2}}$
  
• Planes are perpendicular if aa' + bb' + cc' = 0 and they are parallel
  if $\frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'}$

Planes parallel to a given Plane:
The equation of a plane parallel to the plane ax + by + cz + d = 0
is ax + by + cz + d' = 0. d' is to be found by other given conditions.

15. The angle between a line and Plane :

Let equations of the line be $\frac{x-x_1}{l} = \frac{y-y_1}{m} = \frac{z-z_1}{n}$ and plane be ax + by + cz + d = 0 respectively and $\theta$ be the angle which line makes with the plane.
Then $(\frac{\pi}{2} - \theta)$ is the angle between the line and the normal to the plane.
Sin$\theta = \frac{al + bm + cn}{\sqrt{a^2+b^2+c^2}\sqrt{l^2+m^2+n^2}}$

• If the Line is parallel to the plane, then $\theta = 0$, i.e. if al + bm + cn = 0.
• Line is $\perp$ to the plane if the line is parallel to the normal of the plane, i.e., if $\frac{a}{l} = \frac{b}{m} = \frac{c}{n}$

16. Condition for Line to lie on Plane:

The $\frac{x-x_1}{l} = \frac{y-y_1}{m} = \frac{z-z_1}{n}$ will lie on the plane $Ax + By + Cz + D = 0$ if

• $Al + Bm + Cn = 0$ and
• $Ax_1 + By_1 + Cz_1 + D = 0$

17. Position of two points with respect to a Plane:

Two points P($x_1, y_1, z_1$) & Q($x_2, y_2, z_2$) are on the same or opposite sides of a plane $ax + by + cz + d = 0$ according to the sign of $ax_1+by_1+cz_1+d$ and $ax_2+by_2+cz_2+d$.

• If Signs are the same, then Points P & Q lie on the same side of the plane.
• If Signs are opposite, then Points P & Q lie on the opposite side of the plane.

18. Image of a Point in the Plane:

An image Q($x_2, y_2, z_2$) of a point P ($x_1, y_1, z_1$) in a plane ax + by + cz + d = 0 is
$\frac{x_2-x_1}{a} = \frac{y_2-y_1}{b} = \frac{z_2-z_1}{c} = -2(\frac{ax_1+by_1+cz_1+d}{a^2+b^2+c^2})$
And the coordinates of the foot of perpendicular Q($x_3, y_3, z_3$) of point P ($x_1, y_1, z_1$) on the plane ax + by + cz + d = 0 is

$\frac{x_3-x_1}{a} = \frac{y_3-y_1}{b} = \frac{z_3-z_1}{c} = -(\frac{ax_1+by_1+cz_1+d}{a^2+b^2+c^2})$

19. Condition for the Lines to be Coplanar:

Let the equation of the lines be
$\frac{x-\alpha_1}{l_1} = \frac{y-\beta_1}{m_1} = \frac{z-\gamma_1}{n_1}$ .....(i) and
$\frac{x-\alpha_2}{l_2} = \frac{y-\beta_2}{m_2} = \frac{z-\gamma_2}{n_2}$ .....(ii)

These lines are coplanar if $\begin{vmatrix} \alpha_2-\alpha_1 & \beta_2-\beta_1 & \gamma_2 - \gamma_1 \\ l_1 & m_1 & n_1 \\ l_2 & m_2 & n_2 \\ \end{vmatrix} = 0$
the plane containing the two lines is $\begin{vmatrix} x-\alpha_1 & y-\beta_1 & z - \gamma_1 \\ l_1 & m_1 & n_1 \\ l_2 & m_2 & n_2 \\ \end{vmatrix} = 0$

20. Distance of a Point from the Plane:

Perpendicular distance p, of the point P($x_1, y_1, z_1$) from the plane ax + by + cz + d = 0 is given by
P = $\frac{|ax_1+by_1+cz_1+d|}{\sqrt{(a^2+b^2+c^2)}}$
Distance d between two parallel planes $ax + by + cz + d_1 = 0$ and $ax + by + cz + d_2 = 0$ is
d = $|\frac{d_2 - d_1}{\sqrt{a^2+b^2+c^2}}|$

21. Equation of a Plane through the line of intersection of two planes:

Consider two planes $u = ax + by + cz + d = 0$ and $v = a'x + b'y + c'z + d' = 0.$
The equation $u + \lambda v = 0,$ where $\lambda$ a real parameter, represents the plane passing through the line of intersection of given planes, and if planes are parallel, this represents a plane parallel to them

22. Angle bisectors between two planes:

Let the equations of the two planes be $ax + by + cz + d = 0$ and $px + qy + rz + s = 0.$
Then equations of bisectors of angles between them are given by

$\frac{ax + by + cz + d}{\sqrt{a^2 + b^2 + c^2}} = \plusmn (\frac{px + qy + rz + s}{\sqrt{p^2 + q^2 + r^2}})$

• Equation of bisector of the angle containing origin:
  First, make both constant terms positive.
  Then, the +ve sign gives the bisector of the angle that contains the origin.

• Bisector of acute/obtuse angle:
  First, making both constant terms positive,
  $ap + bq + cr > 0 \Rightarrow$ origin lies in obtuse angle
  $ap + bq + cr < 0 \Rightarrow$ origin lies in acute angle
  

$\color{red} \bold{Related \space Pages:}$
Line and Plane in 3-D Calculators
Vector operation Calculators
Vector Formula sheet