Continuity Formula Sheet

Continuity of a function at a point means that the function's value approaches the same number from both directions as the input approaches that point, ensuring no abrupt changes or gaps in the graph.

Neetesh Kumar | June 02, 2024 $\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space$ Share this Page on:

• 1. Continuous Functions
• 2. Continuity of the Function in an Interval
• 3. Reasons for Discontinuity
• 4. Intermediate Value Theorem

1. Continuous Functions:

A function $f(x)$ is said to be continuous at $x = a$, if
$\lim\limits_{x \to a} f(x)$ exists and is equal to $f(a)$. Symbolically, $f(x)$ is continuous at $x = a$ if
$\lim\limits_{h \to 0} f(a + h) = \lim\limits_{h \to 0} f(a + h) = f(a) \text{ (finite and fixed quantity)}$ where h > 0
i.e. LHL|$_{x=a} =$ RHL|$_{x=a} =$ Value of f(x)$_{x=a} =$ finite and fixed quantity.
At isolated points, functions are considered to be continuous.

2. Continuity of the Function in an Interval:

(a) A function is said to be continuous in $(a, b)$ if $f$ is continuous at each & every point belonging to $(a, b)$.
(b) A function is said to be continuous in a closed interval $[a, b]$ if:

• $f$ is continuous in the open interval $(a, b)$
• $f$ is right continuous at $a$, i.e. $\lim\limits_{x \to a^+} f(x) = f(a)$ (finite quantity)
• $f$ is left continuous at $b$, i.e. $\lim\limits_{x \to b^-} f(x) = f(b)$ (finite quantity)

Note:

• All polynomials, trigonometrical functions, exponential & logarithmic functions are continuous in their domains.
• If $f$ & $g$ are two functions that are continuous at $x = c$ then the function defined by:
  • $F(x) = f(x) \pm g(x)$
  • $F(x) = k f(x)$, $k$ any real number
  • $F(x) = f(x) \cdot g(x)$ are also continuous at $x = c$. Further, if $g(c)$ is not zero, then $F(x) = \frac{f(x)}{g(x)}$ is also continuous at $x = c$.
• If $f$ and $g$ are continuous, then $f \circ g$ and $g \circ f$ are also continuous.

• If f and g are discontinuous at x = c, then f + g, f – g, f.g may still be continuous.
• The sum or difference of a continuous and a discontinuous function is always discontinuous.

3. Reasons for Discontinuity:

(a) Limit does not exist: i.e. $\lim\limits_{x \to a^-} f(x) \neq \lim\limits_{x \to a^+} f(x)$

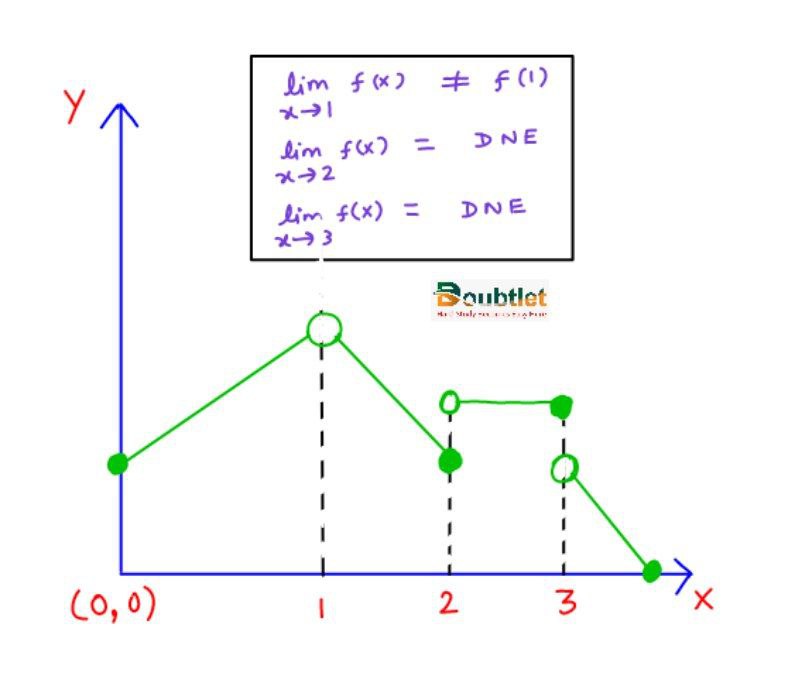
(b) $\lim\limits_{x \to a} f(x) \neq f(a)$

Geometrically, the function's graph will exhibit a break at $x = a$ if the function is discontinuous at $x = a$. The graph, as shown, is discontinuous at $x = 1, 2$, and $3$.

4. Intermediate Value Theorem:

Suppose $f(x)$ is continuous on an interval $I$ and $a$ and $b$ are any two points of $I$. Then if $y_0$ is a number between $f(a)$ and $f(b)$, there exists a number $c$ between $a$ and $b$ such that $f(c) = y_0$.
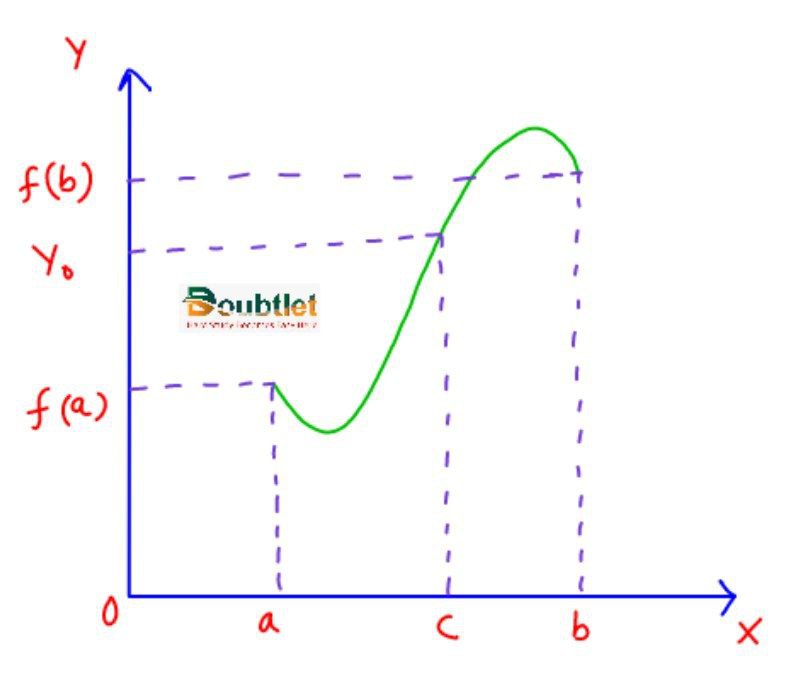
The function f being continuous on [a, b] takes on every value between f(a) and f(b).

$0 \leq a \leq c \leq b$

$f(a) \leq y_0 \leq f(b)$

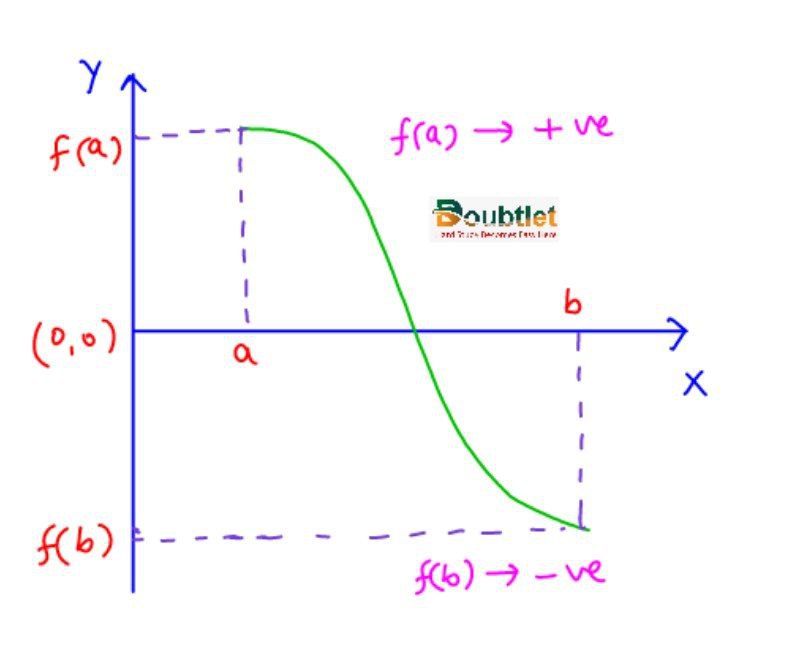
Note that a function f, which is continuous in [a,b], possesses the following property : If $f(a)$ is positive and $f(b)$ is negative, then there exists at least one solution of the equation $f(x) = 0$ in the open interval $(a, b)$.

$\color{red} \bold{Related \space Pages:}$
Relation Formula Sheet
Limit Formula Sheet
Vector operation Calculators
Vector Formula sheet