Mathematical-reasoning Formula Sheet

Mathematical reasoning is the logical process of concluding based on established mathematical principles, rules, and axioms. It involves analyzing and synthesizing information, identifying patterns, and making deductions or inferences to solve problems or prove mathematical statements.

Neetesh Kumar | May 30, 2024 $\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space$ Share this Page on:

• 1. Definition
• 2. Simple Statement
• 3. Compound Statement
• 4. Logical Connectives
• 5. Truth Table
• 6. Tautology and Contradiction
• 7. Compound Statement
• 8. Duality
• 9. Converse, Inverse and Contrapositive of the Conditional Statement
• 10. Negation of Compound Statements
• 11. Algebra of Statements
• 12. Quantified Statements and Quantifiers

1. Definition:

A statement is a declarative sentence that is true or false but not both. A sentence that is an exclamatory, a wish, an imperative, or an interrogative cannot be a statement.
If a statement is true, its truth value is ( T ); if it is false, its truth value is ( F ).

2. Simple Statement:

Any statement whose truth value does not depend on other statements is called a simple statement.

3. Compound Statement:

A statement that combines two or more simple statements is called a compound statement. The simple statements that form a compound statement are known as its sub-statements.

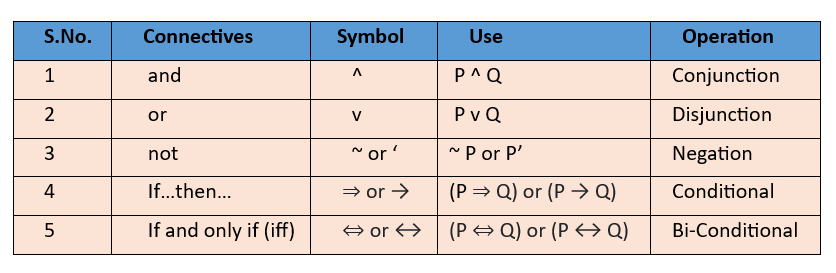
4. Logical Connectives:

The words or phrases which combine simple statements to form a compound statement are called logical connectives.

S.N.	Connectives	Symbol	Use	Operation
1	and	$\land$	( p $\land$ q )	Conjunction
2	or	$\lor$	( p $\lor$ q )	Disjunction
3	not	~ or '	~ p or p'	Negation
4	If ... then ...	$\Rightarrow$ or $\rightarrow$	( p $\Rightarrow$ q ) or ( p $\rightarrow$ q )	Implication or Conditional
5	If and only if (iff)	$\Leftrightarrow$ or $\leftrightarrow$	( p $\Leftrightarrow$ q ) or ( p $\leftrightarrow$ q )	Equivalence or Bi-conditional

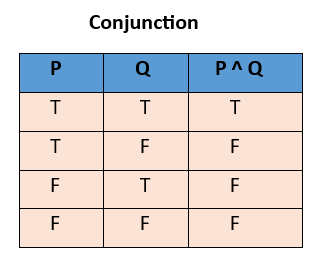
5. Truth Table:

• Conjunction
  
  

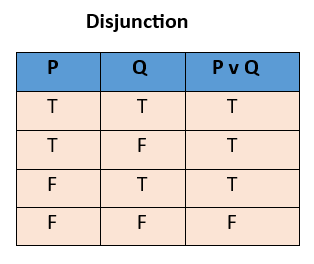
• Disjunction
  
  

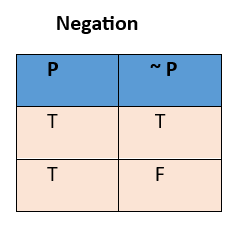
• Negation
  
  

• Conditional
  
  

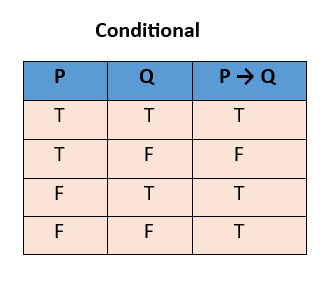
• Biconditional
  
  

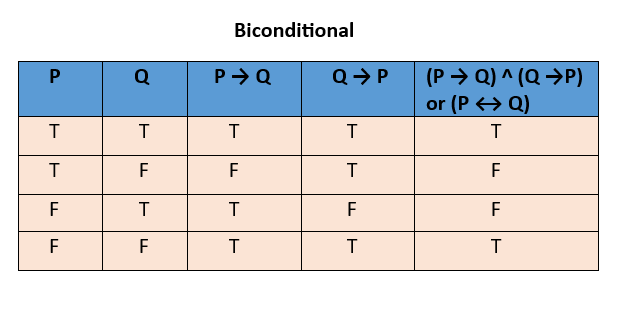
Note: If the compound statement contains ( n ) sub-statements, then its truth table will contain ( $2^n$ ) rows.

6. Logical Equivalence:

Two compound statements $S_1$(p, q, r,...) and $S_2$(p, q, r,....) are said to be logically equivalent or simply equivalent if they have the same truth values for all logical possibilities.

Two statements $S_1$ and $S_2$ are equivalent if they have identical truth tables i.e., the entries in the last column of their truth table are the same. If statements $S_1$ and $S_2$ are equivalent then we write $S_1$ $\equiv$ $S_2$ i.e. $\fcolorbox{red}{yellow}{$p \rightarrow q \equiv$ ~ $p \lor q$}$

7. Tautology and Contradiction:

• Tautology: A statement is considered a tautology if it is true for all logical possibilities i.e.,
  its truth value is always ( T ). It is denoted by ( t ).
• Contradiction/Fallacy: A statement is a contradiction if it is false for all logical possibilities i.e.,
  its truth value is always ( F ). It is denoted by ( c ).

Note: The negation of a tautology is a contradiction, and the negation of a contradiction is a tautology.

8. Duality:

Two compound statements $S_1$ and $S_2$ are said to be duals of each other if one can be obtained from the other by replacing $\land$ by $\lor$ and $\lor$ by $\land$.

If a compound statement contains the special variable t (tautology) and c (contradiction), then we obtain its dual by replacing t by c and c by t in addition to replacing $\land$ by $\lor$ and $\lor$ by $\land$.

Note:

1. The connectives $\land$ and $\lor$ are also called duals of each other.
2. If $S^*$(p,q) ) is the dual of the compound statement ( S(p,q) ) then:
   • $S^*$(~ p, ~ q) $\equiv$ ~ S(p, q)
   • ~ S$^*$(p, q) $\equiv$ S(~ p, ~ q)

9. Converse, Inverse, and Contrapositive of the Conditional Statement p $\rightarrow$ q:

• Converse: The converse of the conditional statement p $\rightarrow$ q is defined as q $\rightarrow$ p.
• Inverse: The inverse of the conditional statement p $\rightarrow$ q is defined as ~ p $\rightarrow$ ~ q ).
• Contrapositive: The contrapositive of the conditional statement p $\rightarrow$ q is defined as ~ q $\rightarrow$ ~ p.

Note: p $\rightarrow$ q $\equiv$ (~ q $\rightarrow$ ~ p) $\equiv$ (~ p $\lor$ q) ).

10. Negation of Compound Statements:

If P and Q are two statements, then:

1. Negation of conjunction: ~(p $\land$ q) $\equiv$ ~ p $\lor$ ~ q )
2. Negation of disjunction: ( ~ (p $\lor$ q) $\equiv$ ~ p $\land$ ~ q )
3. Negation of conditional: ( ~ (p $\rightarrow$ q) $\equiv$ p $\land$ ~ q )
4. Negation of biconditional: ( ~ (p $\leftrightarrow$ q) $\equiv$ (p $\land$ ~ q) $\lor$ (q $\land$ ~ p) $\equiv$ (~ p $\leftrightarrow$ q) $\equiv$ (p $\leftrightarrow$ ~ q) )

As we know that ( p $\leftrightarrow$ q $\equiv$ (p $\rightarrow$ q) $\land$ (q $\rightarrow$ p) ),

~ (p $\leftrightarrow$ q) $\equiv$ ~ [(p $\rightarrow$ q) $\land$ (q $\rightarrow$ p)] $\equiv$ ~ (p $\rightarrow$ q) $\lor$ ~ (q $\rightarrow$ p) $\equiv$ (p $\land$ ~ q) $\lor$ (q $\land$ ~ p)

Note: The above result can also be proved by preparing a truth table for ( ~ (p $\leftrightarrow$ q) ) and ( (p $\land$ ~ q) $\lor$ (q $\land$ ~ p) ).

11. Algebra of Statements:

If (p, q, r) are any three statements, then some laws of the algebra of statements are as follows:

• Idempotent Laws: (a) p $\land$ p $\equiv$ p

  (b) p $\lor$ p $\equiv$ p

• Commutative Laws:

  (a) p $\land$ q $\equiv$ q $\land$ p

  (b) p $\lor$ q $\equiv$ q $\lor$ p

• Associative Laws:

  (a) (p $\land$ q) $\land$ r $\equiv$ p $\land$ (q $\land$ r)

  (b) (p $\lor$ q) $\lor$ r $\equiv$ p $\lor$ (q $\lor$ r)

• Distributive Laws:

  (a) p $\land$ (q $\lor$ r) $\equiv$ (p $\land$ q) $\lor$ (p $\land$ r)

  (b) p $\lor$ (q $\land$ r) $\equiv$ (p $\lor$ q) $\land$ (p $\lor$ r)

• De Morgan Laws:

  (a) ~ (p $\land$ q) $\equiv$ ~ p $\lor$ ~ q

  (b) ~ (p $\lor$ q) $\equiv$ ~ p $\land$ ~ q

• Involution Laws (or Double Negation Laws):

  ~ (~ p) $\equiv$ p

• Identity Laws: If P is a statement and t and c are tautology and contradiction respectively, then:

  (a) p $\land$ t $\equiv$ p

  (b) p $\lor$ t $\equiv$ t

  (c) p $\land$ c $\equiv$ c

  (d) p $\lor$ c $\equiv$ p

• Complement Laws:

  (a) p $\land$ (~ p) $\equiv$ c

  (b) p $\lor$ (~ p) $\equiv$ t

  (c) ~ t $\equiv$ c

  (d) ~ c $\equiv$ t

12. Quantified Statements and Quantifiers:

The words or phrases "All", "Some", "None", "There exists a" are examples of quantifiers.

A statement containing one or more of these words (or phrases) is a quantified statement.

Note: Phrases "There exists a" and "At least one" and the word "some" have the same meaning.

Negation of Quantified Statements:

1. "None" is the negation of " at least one," "some," or "few." Similarly, the negation of "some" is "none".
2. The negation of "some A are B" or "There exists A which is B" is "No A are (is) B" or "There does not exist any A which is B".
3. The negation of "All A are B" is "Some A are not B".

$\color{red} \bold{Related \space Pages:}$
Relation Formula Sheet
Sets Formula Sheet
Vector Formula sheet
Vector operation Calculators