









Straight-line Formula Sheet
This page will help you to revise formulas and concepts of Straight-line instantly for various exams.- Home
- Formula-Sheet
- Straight-line
A straight line in geometry represents the shortest distance between two points and is defined by its constant slope and linear equation, y=mx+b. It extends infinitely in both directions without any curvature.
Neetesh Kumar | May 06, 2024
Share this Page on:
![]()
![]()
![]()
![]()
![]()
- 1. Relation Between Cartesian & Polar Coordinate System
- 2. Distance Formula and its Applications
- 3. Section Formula
- 4. Coordinates of Most commonly used Points
- 5. Area of Triangle
- 6. Condition of Collinearity of three Points
- 7. Equation of Straight Line
- 8. Slope of Line
- 9. Standard forms of equations of Straight Line
- 10. Angle between two Lines
- 11. Length of Perpendicular from a Point on a Line
- 12. Distance between two Parallel lines
- 13. Equation of Lines Parallel & Perpendicular to a given Line
- 14. Straight line making an angle with a given Line
- 15. Position of Two points concerning a given Line
- 16. Concurrency of Lines
- 17. Reflection of a Point
- 18. Transformation of Axes
- 19. Equation of Bisectors of Angles between two lines
- 20. Family of Lines
- 21. General equation and Homogeneous equation of second degree
- 22. Equation of Lines joining the points of Intersection of a Line and a Curve to the Origin
- 23. Standard Results
1. Relation Between Cartesian & Polar Coordinate system:
If (x,y) are Cartesian coordinates of a point P, then x =r cos, y = r sin and r = , =
2. Distance Formula and its Applications:
If A(x, y) and B(x, y) are two points, then AB =
Three given points A, B, and C are collinear when the sum of any two distances out of AB, BC, and CA is equal to the remaining third; otherwise, the points will be the triangle's vertices.
Let A,B,C & D be the four given points in a plane. Then, the quadrilateral will be :
- Square if AB = BC = CD = DA & AC = BD ; AC BD
- Rhombus if AB = BC = CD = DA and AC BD; AC BD
- Parallelogram if AB = DC, BC = AD; AC BD; AC BD
- Parallelogram if AB = DC, BC = AD; AC = BD; AC BD
3. Section Formula :
The coordinates of a point dividing a line joining the points A (x, y) and B (x, y) in the ratio m:n is given by :
Line ax + by + c = 0 divides line joining points P(x, y) & Q(x, y) in ratio =
4. Coordinates of Most commonly used Points:
Let A (x, y) and B (x, y) are vertices of any triangle ABC, then
(i) The centroid is the point of intersection of the medians (line joining the midpoint of sides and opposite vertices).
(ii) Centroid divides the median in the ratio of 2:1
(iii) If G is any internal point of the triangle such that the area of triangles AGB, AGC, and BGC are the same, then G must be centroid.
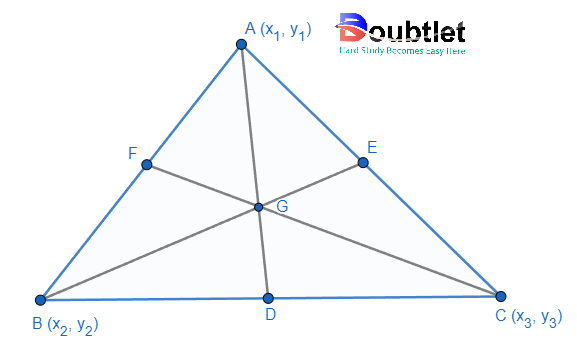
Co-ordinates of centroid G
(i) The incenter is the point of intersection of internal bisectors of the angles of a triangle. Also, a circle's center touches a triangle's sides. Co-ordinates of incenter is I, where a, b, c are the sides of triangle ABC.
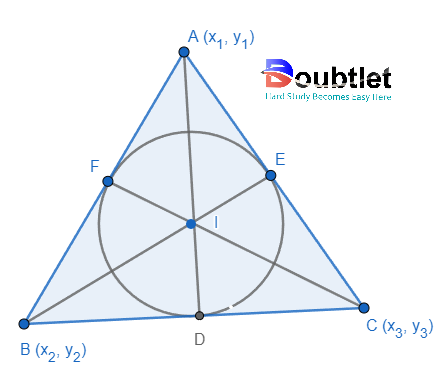
Co-ordinates of incenter I =
Angle bisector divides the opposite sides in the ratio of the remaining sides. e.g.
Incenter divides the angle bisectors in the ratio (b + c) : a, (c + a) : b, (a + b) : c
It is the point of intersection of perpendicular bisectors of the sides of a triangle. If O is the circumcenter of any triangle ABC, then OA2 = OB2 = OC2. Also, it is a circle's center that touches all the vertices of a triangle.
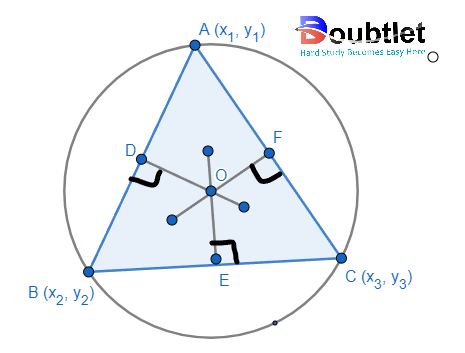
If a triangle is a right angle, then its circumcenter is the midpoint
of the hypotenuse.
Find the perpendicular bisector of any two sides and solve them to find the circumcentre.
It is the point of intersection of the perpendicular drawn from vertices on opposite sides of a triangle and can be obtained by solving the equation of any two altitudes.
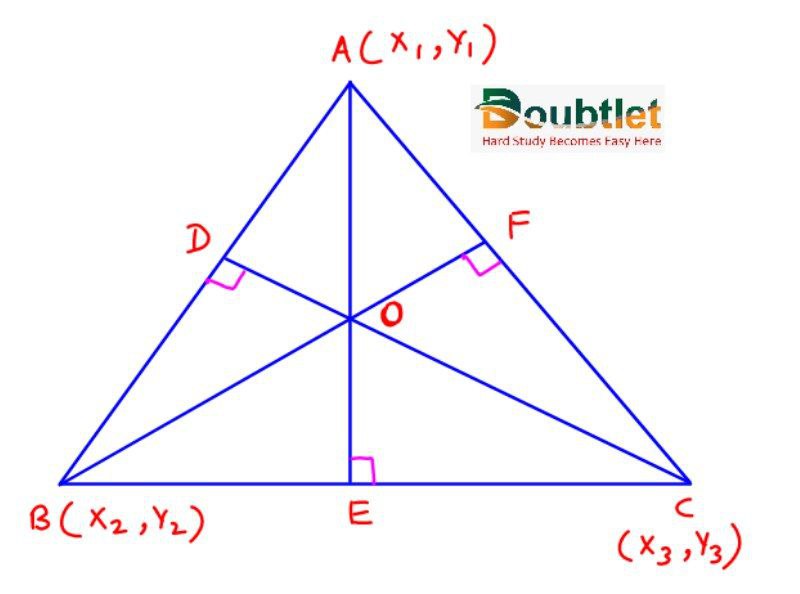
If a triangle is a right-angled triangle, then the orthocenter is where the right angle is formed.
If the triangle is equilateral, then centroid, incentre, orthocenter, and circumcenter coincide.
Orthocentre, centroid, and circumcentre are always collinear, and the centroid divides the line joining orthocentre and circumcentre in the ratio 2:1
In an isosceles triangle, the centroid, orthocentre, incentre, and circumcentre lies on the same line.
The center of the circle, which touches side BC and the extended portions of sides AB and AC, is called the ex-center of triangle ABC with respect to vertex A. It is denoted by I1, and its coordinates are
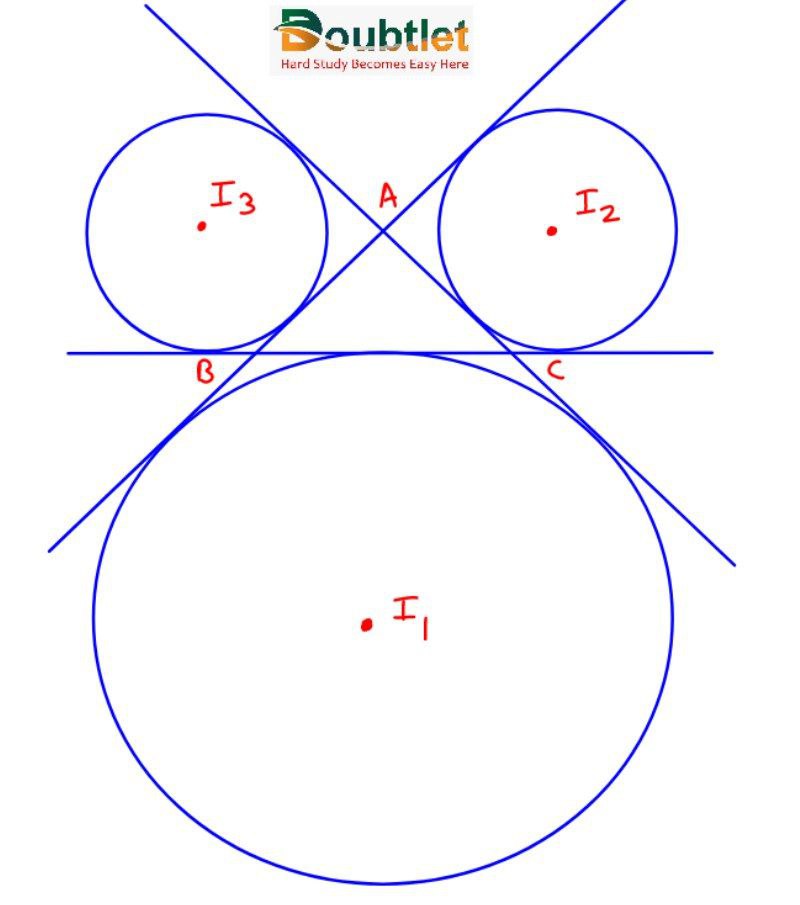
Similarly, ex-centers of ABC with respect to vertices B and C are denoted by and , respectively, and
5. Area of Triangle:
Let A(x, y), B(x, y) and C(x, y) are vertices of a triangle, then
Area of ABC = || =
To remember the above formula, take the help of the following method :
=
If the area of the triangle joining three points is zero, then the points are collinear.
If the altitude of any equilateral triangle is P, then its area =
If 'a' be the side of equilateral triangle, then its area =
Area of quadrilateral whose consecutive vertices are (x, y), (x, y), (x, y), (x, y) is
6. Condition of Collinearity of three Points:
Three points (x, y), (x, y), and (x, y) are collinear if any one of the
the given points lie on the line passing through the remaining two points.
Thus, the required condition is:
= or = or = 0
7. Equation of Straight Line:
A relation between x and y, which is satisfied by the coordinates of every point on a line, is called an equation of the straight line. Remember that every one-degree equation in variables x and y always represents a straight line, i.e., ax + by + c = 0; a & b 0 simultaneously.
Equation of a line parallel to the x-axis at a distance a is y = a or y = – a
Equation of x-axis is y = 0
Equation of line parallel to y-axis at a distance b is x = b or x = – b
Equation of y-axis is x = 0
8. Slope of Line:
If a given line makes an angle (0° 180°, 90°)
with the positive direction of the x-axis, then the slope of this line will be a tan and is usually denoted by the letter, i.e., m = tanθ. The slope of the x-axis and a line parallel to it is zero, and the y-axis and a line parallel to it do not exist.
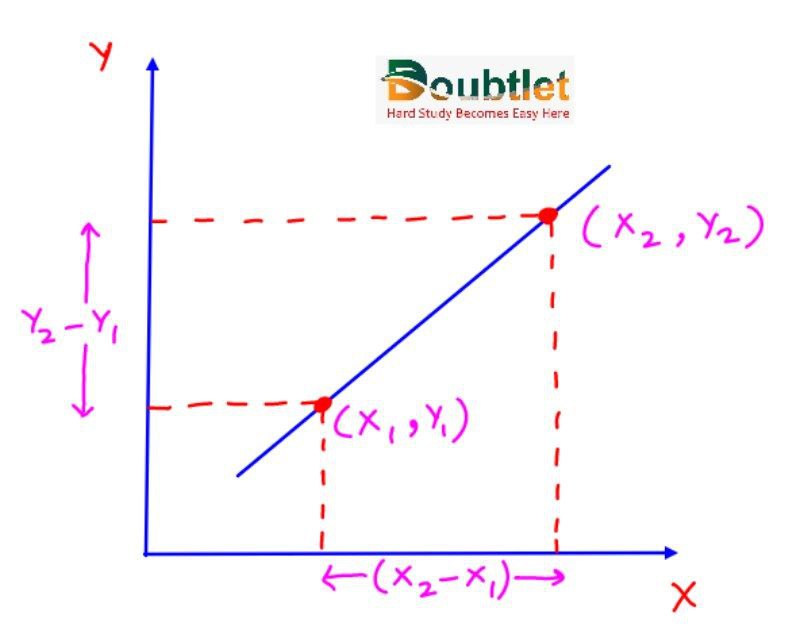
If A (x, y) and B (x, y) & then slope of line AB =
9. Standard forms of Equation of a Straight Line :
(a) Slope Intercept form:
Let m be the slope of a line and c its intercept on the y-axis. Then, the equation of this straight line is written as
(b) Point Slope form:
If m is the slope of a line and it passes through a point (x, y), then its equation is written as
(c) Two-Point form:
Equation of a line passing through two points (x, y) and (x, y) is written as : or = 0
(d) Intercept form:
If a and b are the intercepts made by a line on the axes of x and y, its equation is written as :
(e) Normal form:
If p is the length of the perpendicular on a line from the origin and an angle that this perpendicular makes with a positive x-axis, then the equation of this line is written as : (p is always positive), where 0 < 2
(f) Parametric form:
To find the equation of a straight line that passes through a given point A(h, k) and makes a given angle α with the positive x-axis direction. P(x, y) is any point on the line LAL'.
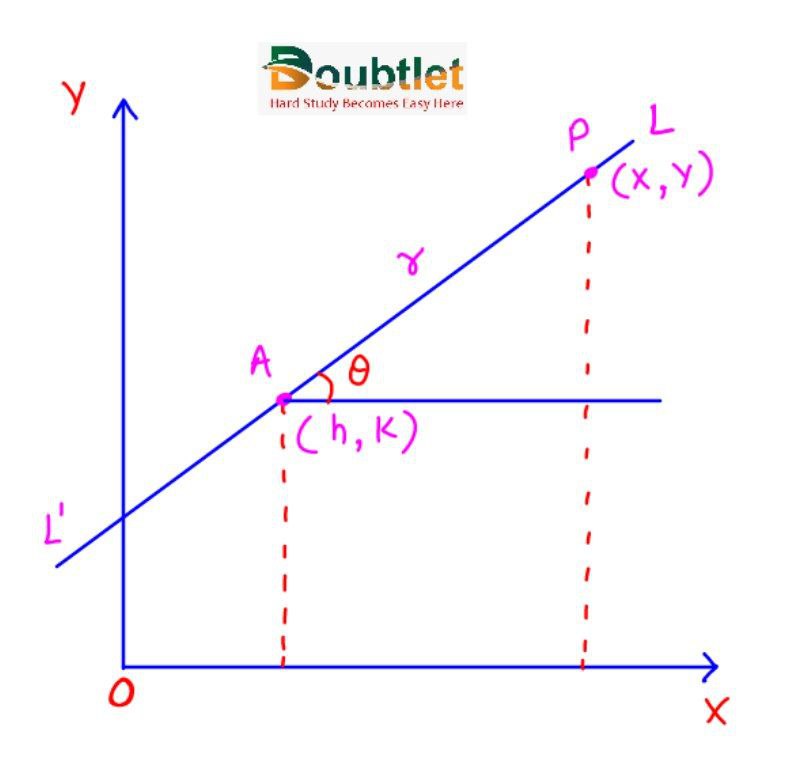
Let AP = r then x – h = r cos, y – k = rsin & = r is the equation of the straight line LAL'.
Any point P on the line will be of the form (h + r cos, k + r sin), where | r | gives the distance of the point P from the fixed point (h, k).
(g) General form:
We know that a first-degree equation in x and y, , always represents a straight line. This form is known as a general form of straight line.
Slope of this line = - = -
Intercept made by this line on x-axis = - and intercept made by this line on y-axis = -
To change the general form of a line to normal form, first take c to the right-hand side and make it positive, then divide the whole equation by
10. Angle between two Lines:
If be the angle between two lines : y = mx + c and y = mx + c then tan =
If equation of lines are and then these lines are:
- Parallel
- Perpendicular
- Coincident
- Intersecting
11. Length of Perpendicular from a Point on a Line:
Length of perpendicular from a point (x, y) on the line ax + by + c = 0 is = ||.
In particular, the length of the perpendicular from the origin on the line ax + by + c = 0 is P = .
12. Distance between two Parallel lines:
The distance between two parallel lines ax + by + c = 0 and
ax + by + c = 0 is
The coefficients of x & y in both equations should be same.
The area of the parallelogram = , where & are distances between two pairs of opposite sides & q is the angle between any two adjacent sides. Note that the area of the parallelogram is bounded by the lines y = mx + c, y = mx + c and y = mx + d, y = mx + d is given by ||.
13. Equation of Parallel & Perpendicular lines to a given Line:
Equation of line parallel to line ax + by + c = 0 is ax + by + = 0
Equation of line perpendicular to line ax + by + c = 0 is bx – ay + k = 0.
Here , k, are parameters, and their values are obtained with the
Additional information was given on the problem.
14. Straight line making a given angle with a Line:
Equations of lines passing through a point (x, y) and making an angle a, with the line y=mx+c, is written as :
15. Position of Two points with respect to a given Line:
Let the given line be ax + by + c = 0 and P(x, y), Q(x, y) be two points.
If the quantities ax + by + c and ax + by + c have the same signs, then both the points P and Q lie on the same side of the line ax + by + c = 0.
If the quantities ax + by + c and ax + by + c have opposite signs, they lie on the opposite sides of the line.
16. Concurrency of Lines:
Three lines ax + by + c = 0; ax + by + c = 0 and ax + by + c = 0 are concurrent if = = 0 If lines are concurrent then = 0 but if = 0 then lines may or may not be concurrent {lines may be parallel}.
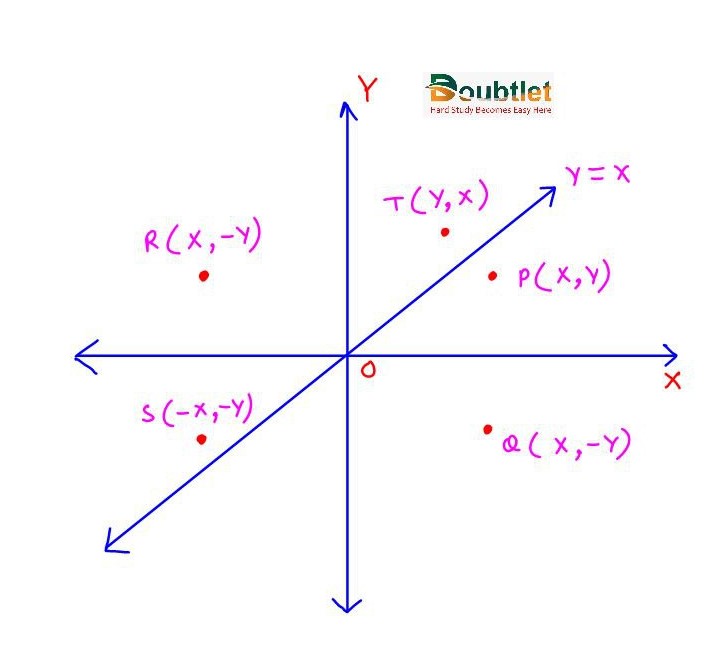
17. Reflection of a Point:
Let P(x,y) be any point, then its image with respect to
(a) x-axis is Q(x, –y)
(b) y-axis is R(–x, y)
(c) origin is S(–x, –y)
(d) line y = x is T(y, x)
18. Transformation of Axes:
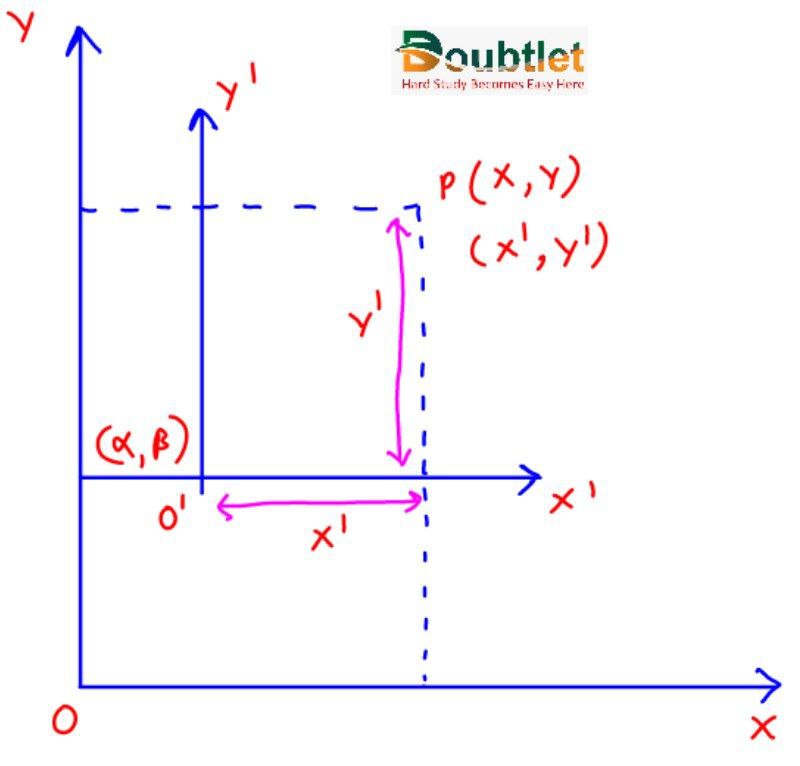
(a) Shifting of origin without rotation of axes:
If coordinates of any point P(x, y) with respect to new origin (α, β) will be (x', y') then
x = x' + α, y = y' + β
or x' = x – α, y' = y – β
Thus, if the origin is shifted to point (α, β) without rotation of axes, a new curve equation can be obtained by putting x + α; in place of x and y + β in place of y.
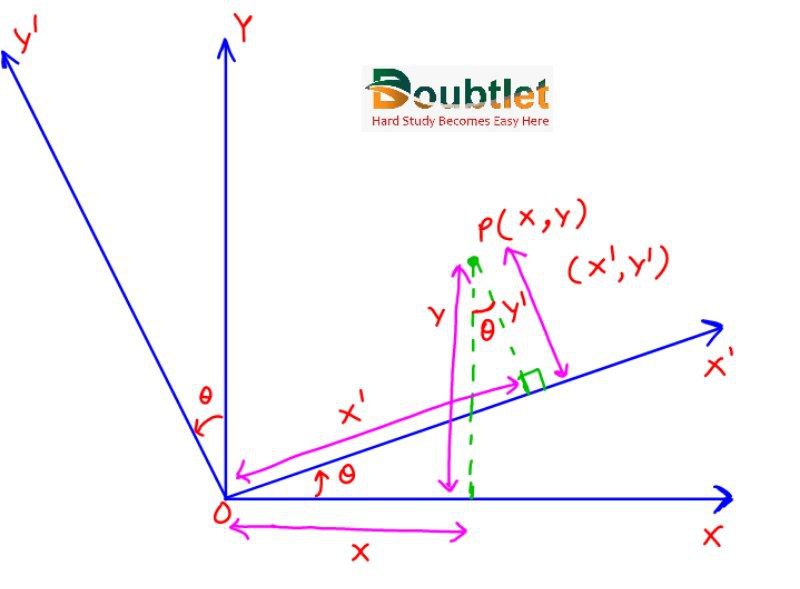
(b) Rotation of axes without shifting the origin:
Let O be the origin. Let P = (x, y) with respect to axes OX and OY and let P = (x', y') with respect to axes OX' and OY', where ∠X'OX = ∠YOY' = θ
then
x = x'cosθ - y'sinθ
y = x'sinθ + y'cosθ
and
x' = xcosθ + ysinθ
y' = -xsinθ + ycosθ
The above relation between (x, y) and (x', y') can be easily obtained with the help of the following table
| New/Old | X | Y |
|---|---|---|
| X' | cos | sin |
| Y' | -sin | cos |
19. Equation of Bisectors of Angles between two lines:
If the equation of two intersecting lines is ax + by + c = 0 and ax + by + c = 0, then the equation of bisectors of the angles between
these lines are written as:
.....(1)
(a) Equation of Bisector of angle containing origin:
If the equation of the lines is written with constant terms and positive, then the equation of the bisectors of the angle containing the origin is obtained by taking the positive sign in (1)
(b) Equation of bisector of acute/obtuse angles:
See whether the two equations' constant terms c1 and c2 are +ve. If not, multiply both sides of the given equation by –1 to make the constant terms positive.
Determine the sign of
| Sign of | For obtuse angle bisector | For acute angle bisector |
|---|---|---|
| + | Use + sign in equation (1) | Use - sign in equation (1) |
| - | Use - sign in equation (1) | Use + sign in equation (1) |
i.e. if > 0, then the bisector corresponding to + sign gives obtuse angle bisector
20. Family of Lines:
If the equation of two lines is P = and Q = , then the equation of the lines passing through the point of intersection of these lines is P + Q = 0 or = 0. The value of is obtained with the help of the additional information given in the problem.
21. General equation and Homogeneous equation of second degree:
A general equation of second degree represent a pair of straight lines if or
= 0
If be the angle between the lines, then tan =
If these lines are:
Parallel, if or if and
Perpendicular, if a + b = 0 i.e. coeff. of + coeff. of = 0.
Homogeneous equation of degree always represent a pair of straight lines whose equations are
y = x y = mx & y = mx
;
These straight lines passes through the origin, and for finding the angle between these lines, the same formula as given for the general equation is used.
The conditions that these lines are :
At right angles to each other is a + b = 0. i.e. co-efficient of x² + co-efficient of y² = 0.
Coincident is h² = ab.
Equally inclined to the axis of x is h = 0 . i.e. coeff.
of xy = 0.
The combined equation of angle bisectors between the lines represented by a homogeneous equation of 2 degree is given by
Pair of straight lines perpendicular to the lines and through origin are given by .
If lines are parallel then distance between them is
22. Equation of Lines joining the points of Intersection of a Line and a Curve to the Origin:
Let the equation of curve be : ax2+ 2hxy + by^2 + 2gx + 2fy + c = 0 ...(i)
and The equation of a straight line be: lx + my + n = 0 ....(ii)
Now, the joint equation of line OP and OQ joining the origin and points of intersection, P, and Q, can be obtained by making equation (i) homogenous with the help of the equation of the line. Thus required equation is given by:
23. Standard Results:
Area of rhombus formed by lines a| x | + b| y | + c = 0 or ax by + c = 0 is
Area of triangle formed by line ax + by + c = 0 and axes is
Co-ordinate of the foot of perpendicular (h, k) from (x, y) to the line ax + by + c = 0 is given by
Image of point (x, y) w.r. to the line ax + by + c = 0 is given by


