









(a) Find at least partial sums of the series. (Round your answers to five decimal places.)
1 2 3 4 5 6 7 8 9 10
(b) Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. (If the quantity diverges, enter DIVERGES.)
(c) If it is divergent, explain why.
- The terms of the series do not approach .
- The sequence of partial sums is divergent.
- The series is convergent.
(a) Find at least partial sums of the series. (Round your answers to five decimal places.)
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
(b) Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. (If the quantity diverges, enter DIVERGES.)
(c) If it is divergent, explain why.
- The terms of the series do not approach .
- The sequence of partial sums is divergent.
- The series is convergent.
Question :
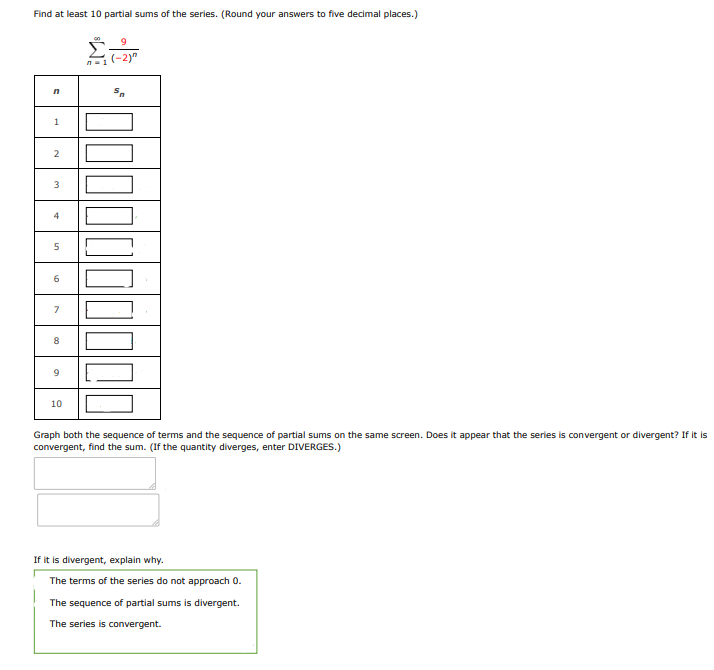
(a) find at least partial sums of the series. (round your answers to five decimal places.)
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
(b) graph both the sequence of terms and the sequence of partial sums on the same screen. does it appear that the series is convergent or divergent? if it is convergent, find the sum. (if the quantity diverges, enter diverges.)
(c) if it is divergent, explain why.
- the terms of the series do not approach .
- the sequence of partial sums is divergent.
- the series is convergent.
Solution:

Neetesh Kumar | December 27, 2024
Calculus Homework Help
This is the solution to Math 1c
Assignment: 11.2 Question Number 3
Contact me if you need help with Homework, Assignments, Tutoring Sessions, or Exams for STEM subjects.
You can see our Testimonials or Vouches from here of the previous works I have done.
Step-by-step solution:
Step 1: Write the series and general term:
The series is:
The -th term of the series is given by:
Step 2: Compute partial sums:
The partial sum is the sum of the first terms:
We calculate for :
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
Step 3: Graph the sequences:
Plot the sequence of terms and the sequence of partial sums .
Step 4: Analyze convergence:
To determine convergence, we observe the behavior of as .
- The sequence of partial sums approaches a limit near . Therefore, the series appears to be convergent.
- The sum of the series is approximately:
Step 5: Explanation for divergence (if applicable):
If the series were divergent, it would fail to meet one of the following conditions:
- The terms would not approach .
- The sequence of partial sums would not settle to a finite value.
In this case, however, the series converges.
Final Answer:
(a)
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
(b)
(c)
Please comment below if you find any error in this solution.
If this solution helps, then please share this with your friends.
Please subscribe to my Youtube channel for video solutions to similar questions.
Keep Smiling :-)
Comments(0)



Leave a comment