









Question :
A tank is full of water. find the work required to pump the water out of the spout. use the fact that water weighs . (assume and ).
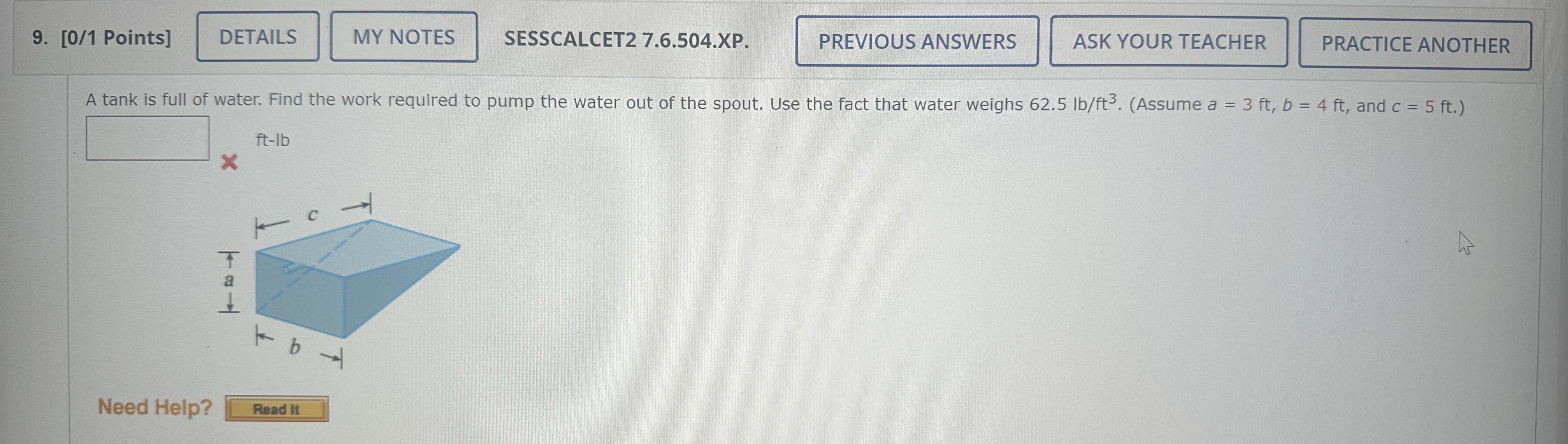
Solution:

Neetesh Kumar | October 12, 2024
Calculus Homework Help
This is the solution to Work done to pump the water out of the tank
Assignment Question
Contact me if you need help with Homework, Assignments, Tutoring Sessions, or Exams for STEM subjects.
You can see our Testimonials or Vouches from here of the previous works I have done.
Step-by-step solution:
The work done to pump the water out of the tank can be computed using the formula:
Given:
- The weight density of water is .
- Dimensions of the tank: .
Step 1: Set up the problem
The base area of the tank is .
The water at height needs to be pumped a distance .
Step 2: Set up the integral
The work done to pump the water out is:
Step 3: Simplify and solve the integral
First, simplify:
Now, compute the integral:
Evaluating the limits:
Step 4: Compute the work
Final Answer:
Please comment below if you find any error in this solution.
If this solution helps, then please share this with your friends.
Please subscribe to my Youtube channel for video solutions to similar questions.
Keep Smiling :-)
Comments(0)



Leave a comment