Neetesh Kumar | January 3, 2025
Calculus Homework Help
This is the solution to Math 1c Assignment: 10.2 Question Number 12 Contact me if you need help with Homework, Assignments, Tutoring Sessions, or Exams for STEM subjects. Testimonials or Vouches from here of the previous works I have done.
Get Homework Help
Step-by-step solution:
Step 1: Formula for arc length of a parametric curve
The arc length of a parametric curve is given by:
L = ∫ a b ( d x d t ) 2 + ( d y d t ) 2 d t L = \int_a^b \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} \, dt L = ∫ a b ( d t d x ) 2 + ( d t d y ) 2 d t
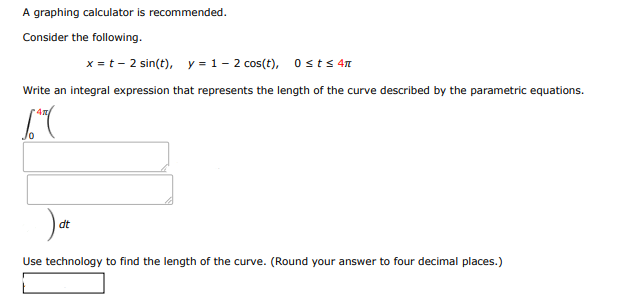
Here, x = t − 2 sin ( t ) x = t - 2\sin(t) x = t − 2 sin ( t ) y = 1 − 2 cos ( t ) y = 1 - 2\cos(t) y = 1 − 2 cos ( t ) t ∈ [ 0 , 4 π ] t \in [0, 4\pi] t ∈ [ 0 , 4 π ]
Step 2: Compute d x d t \frac{dx}{dt} d t d x d y d t \frac{dy}{dt} d t d y
Differentiate x = t − 2 sin ( t ) x = t - 2\sin(t) x = t − 2 sin ( t )
d x d t = 1 − 2 cos ( t ) \frac{dx}{dt} = 1 - 2\cos(t) d t d x = 1 − 2 cos ( t )
Differentiate y = 1 − 2 cos ( t ) y = 1 - 2\cos(t) y = 1 − 2 cos ( t )
d y d t = 2 sin ( t ) \frac{dy}{dt} = 2\sin(t) d t d y = 2 sin ( t )
Step 3: Write the integral for arc length
Substitute d x d t \frac{dx}{dt} d t d x d y d t \frac{dy}{dt} d t d y L L L
L = ∫ 0 4 π ( 1 − 2 cos ( t ) ) 2 + ( 2 sin ( t ) ) 2 d t L = \int_0^{4\pi} \sqrt{\left(1 - 2\cos(t)\right)^2 + \left(2\sin(t)\right)^2} \, dt L = ∫ 0 4 π ( 1 − 2 cos ( t ) ) 2 + ( 2 sin ( t ) ) 2 d t
Simplify the terms inside the square root:
Expand ( 1 − 2 cos ( t ) ) 2 \left(1 - 2\cos(t)\right)^2 ( 1 − 2 cos ( t ) ) 2
( 1 − 2 cos ( t ) ) 2 = 1 − 4 cos ( t ) + 4 cos 2 ( t ) \left(1 - 2\cos(t)\right)^2 = 1 - 4\cos(t) + 4\cos^2(t) ( 1 − 2 cos ( t ) ) 2 = 1 − 4 cos ( t ) + 4 cos 2 ( t )
Expand ( 2 sin ( t ) ) 2 \left(2\sin(t)\right)^2 ( 2 sin ( t ) ) 2
( 2 sin ( t ) ) 2 = 4 sin 2 ( t ) \left(2\sin(t)\right)^2 = 4\sin^2(t) ( 2 sin ( t ) ) 2 = 4 sin 2 ( t )
Combine the terms:
( 1 − 2 cos ( t ) ) 2 + ( 2 sin ( t ) ) 2 = 1 − 4 cos ( t ) + 4 cos 2 ( t ) + 4 sin 2 ( t ) \left(1 - 2\cos(t)\right)^2 + \left(2\sin(t)\right)^2 = 1 - 4\cos(t) + 4\cos^2(t) + 4\sin^2(t) ( 1 − 2 cos ( t ) ) 2 + ( 2 sin ( t ) ) 2 = 1 − 4 cos ( t ) + 4 cos 2 ( t ) + 4 sin 2 ( t )
Use the Pythagorean identity sin 2 ( t ) + cos 2 ( t ) = 1 \sin^2(t) + \cos^2(t) = 1 sin 2 ( t ) + cos 2 ( t ) = 1
( 1 − 2 cos ( t ) ) 2 + ( 2 sin ( t ) ) 2 = 1 − 4 cos ( t ) + 4 ( 1 ) \left(1 - 2\cos(t)\right)^2 + \left(2\sin(t)\right)^2 = 1 - 4\cos(t) + 4(1) ( 1 − 2 cos ( t ) ) 2 + ( 2 sin ( t ) ) 2 = 1 − 4 cos ( t ) + 4 ( 1 )
Simplify further:
( 1 − 2 cos ( t ) ) 2 + ( 2 sin ( t ) ) 2 = 5 − 4 cos ( t ) \left(1 - 2\cos(t)\right)^2 + \left(2\sin(t)\right)^2 = 5 - 4\cos(t) ( 1 − 2 cos ( t ) ) 2 + ( 2 sin ( t ) ) 2 = 5 − 4 cos ( t )
Thus, the arc length is:
L = ∫ 0 4 π 5 − 4 cos ( t ) d t L = \int_0^{4\pi} \sqrt{5 - 4\cos(t)} \, dt L = ∫ 0 4 π 5 − 4 cos ( t ) d t
Step 4: Use technology to evaluate the integral
Using numerical integration, evaluate:
L = ∫ 0 4 π 5 − 4 cos ( t ) d t L = \int_0^{4\pi} \sqrt{5 - 4\cos(t)} \, dt L = ∫ 0 4 π 5 − 4 cos ( t ) d t
After computation:
L ≈ 26.7298 L \approx 26.7298 L ≈ 26.7298
Final Answer:
The integral expression for the arc length is:
L = ∫ 0 4 π 5 − 4 cos ( t ) d t L = \int_0^{4\pi} \boxed{\sqrt{5 - 4\cos(t)} \, dt} L = ∫ 0 4 π 5 − 4 cos ( t ) d t
The length of the curve is approximately:
L ≈ 26.7298 L \approx \boxed{26.7298} L ≈ 26.7298
Please comment below if you find any error in this solution.
If this solution helps, then please share this with your friends.
Please subscribe to my
Youtube channel for video solutions to similar questions.
Keep Smiling :-)














Leave a comment