









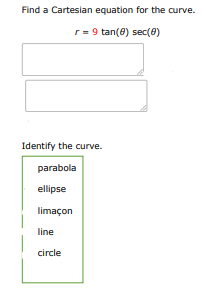
Question :
Find a cartesian equation for the curve:
identify the curve from the following options:
- parabola
- ellipse
- limaçon
- line
- circle
Solution:

Neetesh Kumar | January 2, 2025
Calculus Homework Help
This is the solution to Math 1c
Assignment: 10.3 Question Number 6
Contact me if you need help with Homework, Assignments, Tutoring Sessions, or Exams for STEM subjects.
You can see our Testimonials or Vouches from here of the previous works I have done.
Step-by-step solution:
Step 1: Express in terms of Cartesian coordinates:
The relationships between polar and Cartesian coordinates are:
Given:
Substitute and :
Now multiply both sides by to eliminate and :
From , substitute :
Step 2: Simplify the equation:
Multiply through by to get rid of the denominator:
Step 3: Identify the curve:
The equation represents a parabola.
Final Answer:
The Cartesian equation of the curve is:
The curve is a
Please comment below if you find any error in this solution.
If this solution helps, then please share this with your friends.
Please subscribe to my Youtube channel for video solutions to similar questions.
Keep Smiling :-)
Comments(0)



Leave a comment