









Question :
Find the volume when the region bounded by the curves and is rotated about the x-axis.
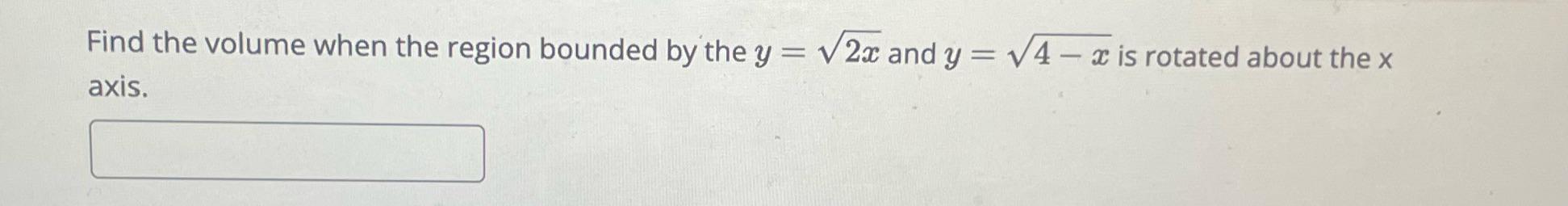
Solution:

Neetesh Kumar | October 08, 2024
Calculus Homework Help
This is the solution to Volume of Solids after Rotation
Assignment Question
Contact me if you need help with Homework, Assignments, Tutoring Sessions, or Exams for STEM subjects.
You can see our Testimonials or Vouches from here of the previous works I have done.
Step-by-step solution:
To find the volume of the solid obtained by rotating the region between two curves about the x-axis, we use the formula for the volume of revolution:
Where:
- is the upper curve,
- is the lower curve,
- and are the bounds of integration.
Here, the two functions are:
We need to find the points where the curves intersect to determine the limits of integration. We set the curves equal to each other to find the intersection points:
Squaring both sides:
Thus, the region is bounded between and .
Now, the volume is given by:
Simplifying:
Now, integrate:
Substitute the limits:
Final Answer:
Thus, the volume is:
Please comment below if you find any error in this solution.
If this solution helps, then please share this with your friends.
Please subscribe to my Youtube channel for video solutions to similar questions.
Keep Smiling :-)
Comments(0)



Leave a comment