









Use the Alternating Series Estimation Theorem or Taylor's Inequality to estimate the range of values of for which the given approximation is accurate to within the stated error. Check your answer graphically. (Enter your answer using interval notation. Round your answers to three decimal places.)
Use the Alternating Series Estimation Theorem or Taylor's Inequality to estimate the range of values of for which the given approximation is accurate to within the stated error. Check your answer graphically. (Enter your answer using interval notation. Round your answers to three decimal places.)
Question :
Use the alternating series estimation theorem or taylor's inequality to estimate the range of values of for which the given approximation is accurate to within the stated error. check your answer graphically. (enter your answer using interval notation. round your answers to three decimal places.)
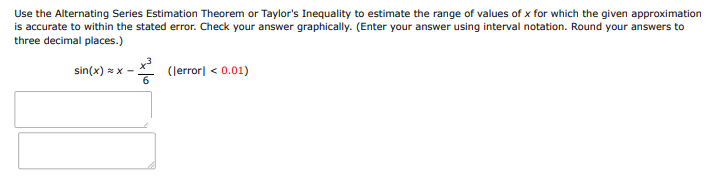
Solution:

Neetesh Kumar | December 22, 2024
Calculus Homework Help
This is the solution to Math 1c
Assignment: 11.11 Question Number 7
Contact me if you need help with Homework, Assignments, Tutoring Sessions, or Exams for STEM subjects.
You can see our Testimonials or Vouches from here of the previous works I have done.
Step-by-step solution:
Step 1: Recall the Taylor series for :
The Taylor series expansion for is:
The approximation given is:
This truncates the series after the second term, so the next term in the series (the remainder term) is:
Step 2: Use Taylor's Inequality to bound the error:
Taylor's Inequality states that the error of the approximation is bounded by the magnitude of the first omitted term. Thus, the error is:
We need this error to satisfy:
Step 3: Solve for :
Rearrange the inequality:
Multiply through by :
Take the fifth root of both sides:
Using a calculator:
Thus, the range of is:
Step 4: Express the range in interval notation:
The range of values of for which the error is less than is:
Final Answer:
The range of is:
Please comment below if you find any error in this solution.
If this solution helps, then please share this with your friends.
Please subscribe to my Youtube channel for video solutions to similar questions.
Keep Smiling :-)
Comments(0)



Leave a comment