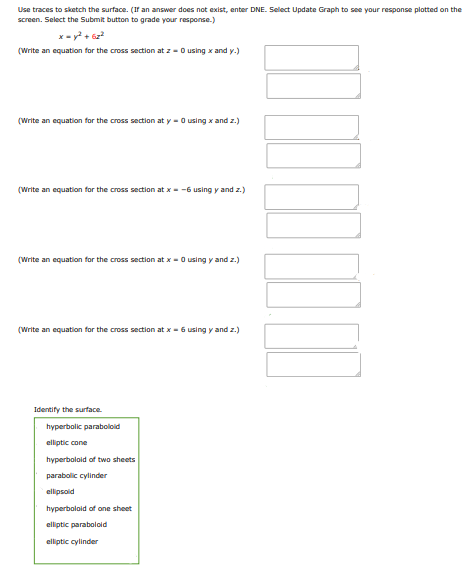
Use traces to sketch the surface. (If an answer does not exist, enter DNE. Select Update Graph to see your response plotted on the screen. Select the Submit button to grade your response.) $x = y^2 + 6z^2$

Find:

• (i) (Write an equation for the cross section at $z = 0$ using $x$ and $y$.)

• (ii) (Write an equation for the cross section at $y = 0$ using $x$ and $z$.)

• (iii) (Write an equation for the cross section at $x = -6$ using $y$ and $z$.)

• (iv) (Write an equation for the cross section at $x = 0$ using $y$ and $z$).

• (v) (Write an equation for the cross section at $x = 6$ using $y$ and $z$).

Identify the surface

• hyperbolic paraboloid
• elliptic cone
• hyperboloid of two sheets
• parabolic cylinder
• ellipsoid
• hyperboloid of one sheet
• elliptic paraboloid
• elliptic cylinder

Neetesh Kumar | December 15, 2024

Calculus Homework Help

This is the solution to Math 1C
Assignment: 12.6 Question Number 8
Contact me if you need help with Homework, Assignments, Tutoring Sessions, or Exams for STEM subjects.
You can see our Testimonials or Vouches from here of the previous works I have done.

Get Homework Help

---

Step-by-step solution:

Step 1: Analyze the given equation

The equation of the surface is: $x = y^2 + 6z^2.$

This represents an elliptic paraboloid since it is quadratic in both $y$ and $z$ and linear in $x$.

Step 2: Find the cross sections

(i) Cross section at $z = 0$

Substitute $z = 0$ into the equation $x = y^2 + 6z^2$:

Answer:

$\boxed{x = y^2}$

This is a parabola opening along the $x$-axis in the $xy$-plane.

(ii) Cross section at $y = 0$

Substitute $y = 0$ into the equation $x = y^2 + 6z^2$:

Answer:

$\boxed{x = 6z^2}$

This is a parabola opening along the $x$-axis in the $xz$-plane.

(iii) Cross section at $x = -6$

Substitute $x = -6$ into the equation $x = y^2 + 6z^2$: $-6 = y^2 + 6z^2.$

Rearrange: $y^2 + 6z^2 = -6.$

This equation has no real solutions since the left-hand side is always non-negative while the right-hand side is negative. Therefore, the cross section does not exist:

Answer:

$\boxed{\text{DNE}}$

(iv) Cross section at $x = 0$

Substitute $x = 0$ into the equation $x = y^2 + 6z^2$: $0 = y^2 + 6z^2.$

Rearrange: $y^2 + 6z^2 = 0.$

Answer:

$\boxed{y^2 + 6z^2 = 0}$

The only solution is $y = 0$ and $z = 0$, so this is a single point at the origin.

(v) Cross section at $x = 6$

Substitute $x = 6$ into the equation $x = y^2 + 6z^2$: $6 = y^2 + 6z^2.$

Rearrange: $y^2 + 6z^2 = 6.$

Answer:

$\boxed{y^2 + 6z^2 = 6}$

This represents an ellipse in the $yz$-plane.

Step 3: Identify the surface

The surface $x = y^2 + 6z^2$ is an elliptic paraboloid.

Answer:

$\boxed{\text{elliptic paraboloid}}$

Final Answer:

(i) Cross section at $z = 0$

$\boxed{x = y^2}$

(ii) Cross section at $y = 0$

$\boxed{x = 6z^2}$

(iii) Cross section at $x = -6$

$\boxed{\text{DNE}}$

(iv) Cross section at $x = 0$

$\boxed{y^2 + 6z^2 = 0}$

(v) Cross section at $x = 6$

$\boxed{y^2 + 6z^2 = 6}$

Identify the surface

$\boxed{\text{elliptic paraboloid}}$

Please comment below if you find any error in this solution.
If this solution helps, then please share this with your friends.
Please subscribe to my Youtube channel for video solutions to similar questions.
Keep Smiling :-)