









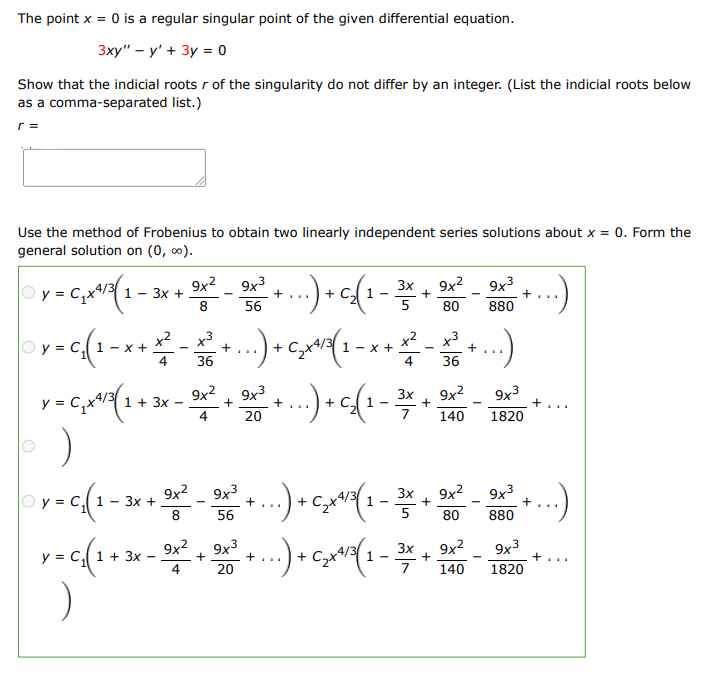
The point is a regular singular point of the given differential equation:
-
(a) Show that the indicial roots of the singularity do not differ by an integer. (List the indicial roots below as a comma-separated list.)
-
(b) Use the method of Frobenius to obtain two linearly independent series solutions about . Form the general solution on .
The point is a regular singular point of the given differential equation:
-
(a) Show that the indicial roots of the singularity do not differ by an integer. (List the indicial roots below as a comma-separated list.)
-
(b) Use the method of Frobenius to obtain two linearly independent series solutions about . Form the general solution on .
Question :
The point is a regular singular point of the given differential equation:
-
(a) show that the indicial roots of the singularity do not differ by an integer. (list the indicial roots below as a comma-separated list.)
-
(b) use the method of frobenius to obtain two linearly independent series solutions about . form the general solution on .
Solution:

Neetesh Kumar | October 24, 2024
Differential Equation Homework Help
This is the solution to Math 2A, section 13Z, Fall 2023 | WebAssign
Math002ACh6Sec03 (Homework) Question - 4
Contact me if you need help with Homework, Assignments, Tutoring Sessions, or Exams for STEM subjects.
You can see our Testimonials or Vouches from here of the previous works I have done.
Step-by-step solution:
Part (a): Indicial Roots
The given differential equation is:
This second-order linear differential equation has a regular singular point at .
We will apply the Frobenius method to find the indicial equation and the roots.
Step 1: Rewrite the Equation in Standard Form
Divide the entire equation by to obtain the standard form:
Now, compare this with the general form:
From this, we identify:
Step 2: Frobenius Method
Assume a solution of the form:
Substitute this into the differential equation and collect terms for the lowest power of . The indicial equation comes from the coefficient of the lowest power of .
Step 3: Indicial Equation
The indicial equation is obtained from the lowest power of , typically involving and terms with . After solving, we get the roots of the indicial equation.
The indicial equation simplifies to:
Solving this gives the indicial roots:
Thus, the indicial roots are:
These roots do not differ by an integer.
Part (b): Series Solution and General Solution
We now use the Frobenius method to find two linearly independent series solutions around .
Step 1: First Solution
We substitute into the series and solve for the first root . The first solution has the form:
Step 2: Second Solution
For the second root , the second linearly independent solution will have the form:
Final Answer:
The general solution to the differential equation is a combination of the two independent solutions:
From the given options, this corresponds to the Last option:
Please comment below if you find any error in this solution.
If this solution helps, then please share this with your friends.
Please subscribe to my Youtube channel for video solutions to similar questions.
Keep Smiling :-)
Comments(0)



Leave a comment