
Neetesh Kumar | October 24, 2024
Differential Equation Homework Help
This is the solution to Math 2A, section 13Z, Fall 2023 | WebAssign
Math002ACh6Sec02 (Homework) Question - 5
Contact me if you need help with Homework, Assignments, Tutoring Sessions, or Exams for STEM subjects.
You can see our Testimonials or Vouches from here of the previous works I have done.
Get Homework Help
Step-by-step solution:
We are tasked with solving the given second-order differential equation using the power series method and satisfying the initial conditions.
Step 1: Assume a Power Series Solution
We assume the solution is of the form:
y(x)=n=1∑∞anxn
Then, we have the following expressions for the derivatives of y(x):
- First derivative:
y′(x)=n=1∑∞nanxn−1
- Second derivative:
y′′(x)=n=1∑∞n(n−1)anxn−2
Step 2: Substitute into the Differential Equation
Now, substitute the power series expressions for y(x), y′(x), and y′′(x) into the differential equation:
(x−1)y′′(x)−xy′(x)+y(x)=0
Substitute y′′(x), y′(x), and y(x) into the equation:
(x−1)n=1∑∞n(n−1)anxn−2−xn=1∑∞nanxn−1+n=0∑∞anxn=0
We expand each term:
- First term: (x−1)y′′(x)
(x−1)n=1∑∞n(n−1)anxn−2=n=2∑∞n(n−1)anxn−1−n=2∑∞n(n−1)anxn−2
- Second term: −xy′(x)
−xn=1∑∞nanxn−1=−n=1∑∞nanxn
- Third term: y(x)
n=1∑∞anxn
Now combine the three terms:
n=1∑∞n(n−1)anxn−1−n=2∑∞n(n−1)anxn−2−n=1∑∞nanxn+n=0∑∞anxn=0
Substitute (n = (n+1)) in the first term and (n = (n + 2)) in the second term.
Rewriting the above expression again:
n=1∑∞(n+1)(n)an+1xn−n=0∑∞(n+2)(n+1)an+2xn−n=1∑∞nanxn+n=0∑∞anxn=0
Now we have to make all summation terms starting from (n = 1)
n=1∑∞(n+1)(n)an+1xn−2a2−n=1∑∞(n+2)(n+1)an+2xn−n=1∑∞nanxn+a0+n=1∑∞anxn=0
Rearranging the above expression:
(a0−2a2)+n=1∑∞(n+1)(n)an+1xn−n=1∑∞(n+2)(n+1)an+2xn−n=1∑∞nanxn+n=1∑∞anxn=0
After solving further:
(a0−2a2)+n=1∑∞((n2+n)an+1−(n2+3n+2)an+2+(1−n)an)xn=0
Comparing coefficients of constants terms:
a0−2a2=0⇒a2=2a0
Comparing coefficients of xn term:
an+2=n2+3n+2(n2+n)an+1−(n−1)an, where n≥1
For n=1⇒a3=3a2=6a0=1.2.3a0
For n=2⇒a4=126a3−a2=24a0=1.2.3.4a0
For n=3⇒a5=2012a4−2a3=120a0=1.2.3.4.5a0
WE know that
y(x)=n=1∑∞anxn=a0+a1x+a2x2+a3x3+a4x4+a5x5+....∞
Replacing the values of coefficients in terms of a0
y(x)=n=1∑∞anxn=a0(1+1.2x2+1.2.3x3+1.2.3.4x4+1.2.3.4.5x5+....∞)+a1x
y(x)=n=1∑∞anxn=a0(1+2!x2+3!x3+4!x4+5!x5+....∞)+a1x
We know that ex=1+x+2!x2+3!x3+....
y(x)=a0(ex−x)+a1x
Step 3: Apply the Initial Conditions
Using the given initial conditions y(0)=−2 and y′(0)=5, we know the following:
- From y(0)=−2: this implies that a0=−2.
y′(x)=a0(ex−1)+a1
- From y′(0)=5: this implies that a1=5.
Step 5: Summing the Power Series
y(x)=−2(ex−x)+5x
After simplifying
y(x)=7x−2ex
Final Answer:
The final solution, formatted as an elementary function, is:
y(x)=7x−2ex
Please comment below if you find any error in this solution.
If this solution helps, then please share this with your friends.
Please subscribe to my
Youtube channel for video solutions to similar questions.
Keep Smiling :-)










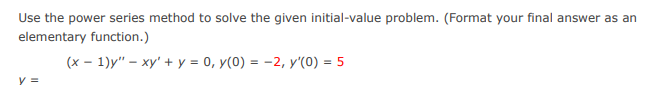




Leave a comment