Without solving, match a solution curve of $y'' + y = f(x)$ shown in the figure with one of the following functions: (i) $f(x) = 1$ (ii) $f(x) = e^{-x}$ (iii) $f(x) = e^{x}$
(iv) $f(x) = \sin(2x)$ (v) $f(x) = e^{x} \sin(x)$ (vi) $f(x) = \sin(x)$

Briefly discuss your reasoning.

Question :

Without solving, match a solution curve of $y'' + y = f(x)$ shown in the figure with one of the following functions: (i) $f(x) = 1$ (ii) $f(x) = e^{-x}$ (iii) $f(x) = e^{x}$ (iv) $f(x) = \sin(2x)$ (v) $f(x) = e^{x} \sin(x)$ (vi) $f(x) = \sin(x)$

briefly discuss your reasoning.

Without solving, match a solution curve of y'' + y = f(x) shown in the figur | Doubtlet.com

Solution:

Neetesh Kumar | November 06, 2024

Differential Equation Homework Help

This is the solution to Math 2A, section 13Z, Fall 2023 | WebAssign
Math002ACh4Sec04 (Homework) Question - 7
Contact me if you need help with Homework, Assignments, Tutoring Sessions, or Exams for STEM subjects.
You can see our Testimonials or Vouches from here of the previous works I have done.

Get Homework Help

Step-by-Step-Solution:

To match the solution curves of the differential equation ( y'' + y = f(x) ) with the provided functions based on the graph, we can analyze the behavior of each function and how it relates to the general characteristics of the solutions to the differential equation.

Breakdown of Each Function

Constant Functions:
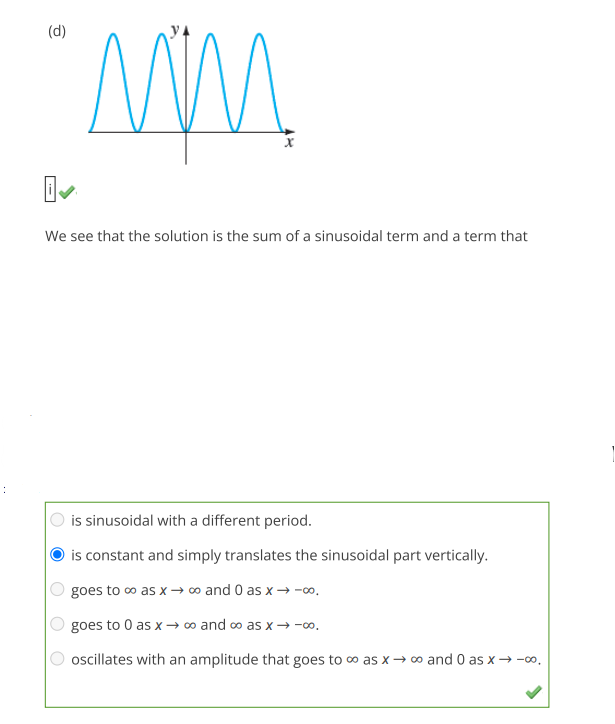
- (i) ( f(x) = 1 ): The solution will be a sinusoidal function oscillating around the value 1, with a constant vertical shift.
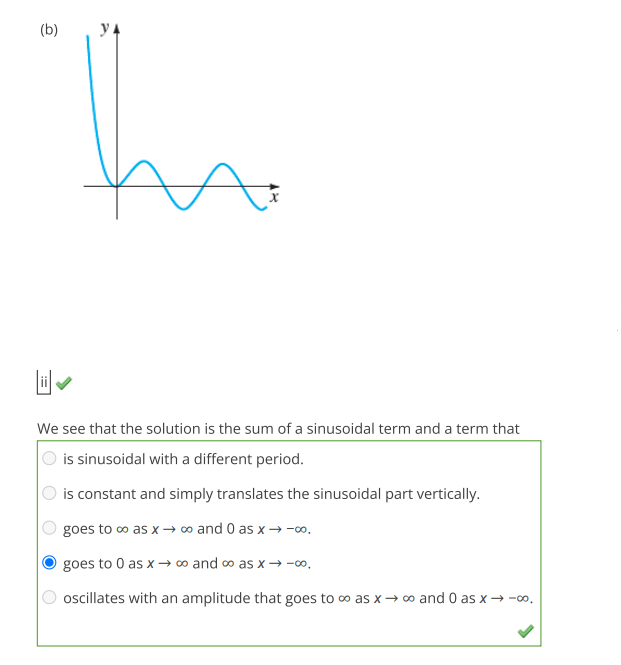
- (ii) ( f(x) = e^{-x} ): The solution will likely approach zero as ( x \to \infty ) and will not oscillate. Instead, it will decay towards 0, which will look like a damped oscillation.
Exponential Functions:
- (iii) ( f(x) = e^x ): The solution will tend to grow indefinitely, which could cause the graph to rise sharply without bound.
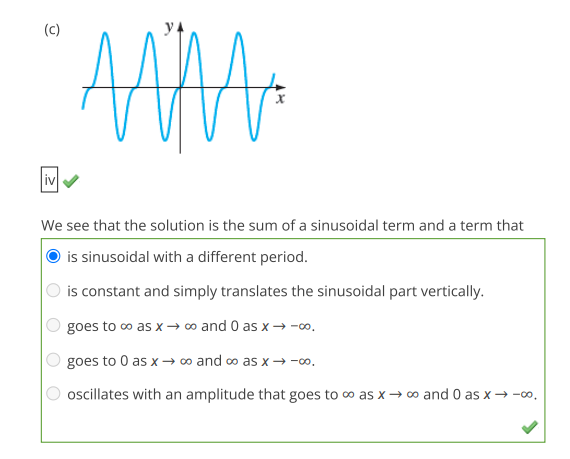
- (iv) ( f(x) = \sin(2x) ): The solution will oscillate with a period of ( \pi ) and will have maximum and minimum values of 1 and -1.
Sinusoidal Functions:
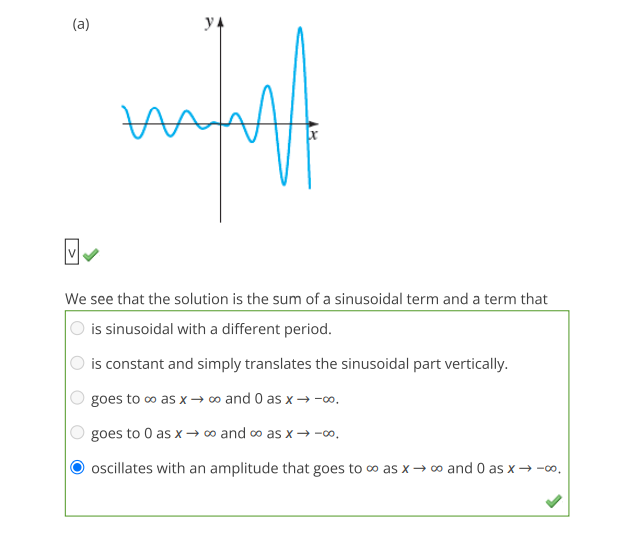
- (v) ( f(x) = e^x \sin(x) ): This function oscillates with growing amplitude due to the ( e^x ) factor, resulting in a sinusoidal wave that increases in magnitude.
- (vi) ( f(x) = \sin(x) ): Similar to (iv), it will oscillate but with a period of ( 2\pi ).

Matching Functions to Curves

Now, based on the figure provided:

If the curve oscillates around a constant value (like 1), then it is likely a match for (i) ( f(x) = 1 ).
If the curve has a damped oscillatory behavior, it aligns with (ii) ( f(x) = e^{-x} ).
If the curve is purely sinusoidal with no decay or growth, it matches (vi) ( f(x) = \sin(x) ).
If the curve shows fast oscillations, it may match (iv) ( f(x) = \sin(2x) ).
If the curve oscillates but increases indefinitely, it corresponds to (v) ( f(x) = e^x \sin(x) ).

Reasoning

Identify if the curve oscillates, grows, or decays.
Determine the frequency of oscillation and if it is sinusoidal or exponential.
Compare the general shape and asymptotic behavior with the expected behavior of the given functions.

Please comment below if you find any error in this solution.
If this solution helps, then please share this with your friends.
Please subscribe to my Youtube channel for video solutions to similar questions.
Keep Smiling :-)