Let $A = \begin{bmatrix} -1 & 2 \\ 2 & 1 \\ 1 & 2 \end{bmatrix}$ and $b = \begin{bmatrix} 5 \\ -4 \\ 4 \end{bmatrix}$.

The orthogonal projection of $b$ onto $\text{Col}(A)$ and the least-squares solution of $A\mathbf{x} = \mathbf{b}$ are:

Neetesh Kumar | October 21, 2024

Linear Algebra Homework Help

This is the solution to Math2B Course: Linear Algebra
Final Exam Question Number 26
Contact me if you need help with Homework, Assignments, Tutoring Sessions, or Exams for STEM subjects.
You can see our Testimonials or Vouches from here of the previous works I have done.

Get Linear Algebra Homework Help

---

Step-by-step solution:

Step 1: Compute the orthogonal projection of $\mathbf{b}$ onto $\text{Col}(A)$

Matrix Multiplication Calculator

To compute the orthogonal projection of $\mathbf{b}$ onto the column space of $A$, we use the formula:

$\text{Proj}_{\text{Col}(A)}(\mathbf{b}) = A(A^T A)^{-1} A^T \mathbf{b}$

First, compute $A^T A$:

$A^T A = \begin{bmatrix} -1 & 2 & 1 \\ 2 & 1 & 2 \end{bmatrix} \begin{bmatrix} -1 & 2 \\ 2 & 1 \\ 1 & 2 \end{bmatrix} = \begin{bmatrix} 6 & 2 \\ 2 & 9 \end{bmatrix}$

Next, compute $A^T \mathbf{b}$:

$A^T \mathbf{b} = \begin{bmatrix} -1 & 2 & 1 \\ 2 & 1 & 2 \end{bmatrix} \begin{bmatrix} 5 \\ -4 \\ 4 \end{bmatrix} = \begin{bmatrix} -5 + (-8) + 4 \\ 10 + (-4) + 8 \end{bmatrix} = \begin{bmatrix} -9 \\ 14 \end{bmatrix}$

Now, compute $(A^T A)^{-1}$:

$(A^T A)^{-1} = \begin{bmatrix} 6 & 2 \\ 2 & 9 \end{bmatrix}^{-1} = \begin{bmatrix} \frac{9}{50} & \frac{-1}{25} \\ \frac{-1}{25} & \frac{3}{25} \end{bmatrix}$

Now, compute the projection:

$\text{Proj}_{\text{Col}(A)}(\mathbf{b}) = A \begin{bmatrix} \frac{9}{50} & \frac{-1}{25} \\ \frac{-1}{25} & \frac{3}{25} \end{bmatrix} \begin{bmatrix} -9 \\ 14 \end{bmatrix} = A \begin{bmatrix} -\frac{109}{50} \\ \frac{51}{25} \end{bmatrix} = A \begin{bmatrix} -2.18 \\ 2.04 \end{bmatrix}$

Multiplying $A$ with this result:

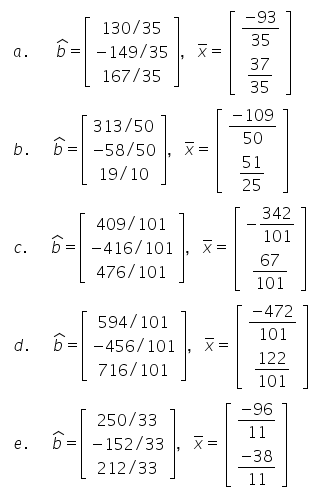
$\text{Proj}_{\text{Col}(A)}(\mathbf{b}) = \begin{bmatrix} -1 & 2 \\ 2 & 1 \\ 1 & 2 \end{bmatrix} \begin{bmatrix} -\frac{109}{50} \\ \frac{51}{25} \end{bmatrix} = \text{Proj}_{\text{Col}(A)}(\mathbf{b}) = \begin{bmatrix} \frac{313}{50} \\ -\frac{58}{25} \\ \frac{19}{10} \end{bmatrix}$

Step 2: Solve the least-squares solution $A\mathbf{x} = \mathbf{b}$

The least-squares solution can be found by solving:

$\mathbf{x} = (A^T A)^{-1} A^T \mathbf{b}$

We already computed $A^T A = \begin{bmatrix} 6 & 2 \\ 2 & 9 \end{bmatrix}$, $(A^T A)^{-1} = \begin{bmatrix} \frac{9}{50} & \frac{-1}{25} \\ \frac{-1}{25} & \frac{3}{25} \end{bmatrix}$, and $A^T \mathbf{b} = \begin{bmatrix} -9 \\ 14 \end{bmatrix}$.

Now compute:

$\mathbf{x} = \begin{bmatrix} \frac{9}{50} & \frac{-1}{25} \\ \frac{-1}{25} & \frac{3}{25} \end{bmatrix} \begin{bmatrix} -9 \\ 14 \end{bmatrix} = \begin{bmatrix} \frac{-109}{50} \\ \frac{51}{25} \end{bmatrix} = \begin{bmatrix} -2.18 \\ 2.04 \end{bmatrix}$

Final Answer:

The correct answer is Option - B

• The orthogonal projection of $\mathbf{b}$ onto $\text{Col}(A)$ is $\begin{bmatrix} \frac{313}{50} \\ -\frac{58}{25} \\ \frac{19}{10} \end{bmatrix}$
• The least-squares solution is $\mathbf{x} = \begin{bmatrix} \frac{-109}{50} \\ \frac{51}{25} \end{bmatrix}$

---

Please comment below if you find any error in this solution.
If this solution helps, then please share this with your friends.
Please subscribe to my Youtube channel for video solutions to similar questions.
Keep Smiling :-)